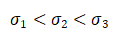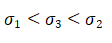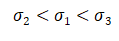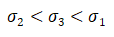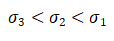一、大纲考点:
(1)平均值
(2)方差与标准差
(3)数据的图表表示直方图,饼图,数表.
本章历年考1个题目,试题主要考察三个方面:
1、平均值和方差的计算;
2、方差的大小含义;
3、常见图表的含义.
1.平均值
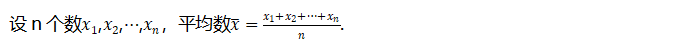
2.众数
在一组数据中,出现次数最多的数据.
3.中位数
将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数).
【重要考向】
1.基本概念
【思路】根据、众数、中位数的概念进行分析判断.
2.一组数平均值计算
【思路】根据平均值的定义,先求出总和,再除以个数得到平均值.为了简化计算,可以将每个数都减去m,求出剩余数的平均值,再加上m即可.
【2018.T2真题回顾】
1、为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:
男员工年龄(岁) | 23 26 28 30 32 34 36 38 41 |
女员工年龄(岁) | 23 25 27 27 29 31 |
根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是()(单位︰岁)
A.32,30
B.33,29.5
C.32,27
D.30,27
E.29.5,27

3.加权平均值计算
【思路】若已知各部分的平均值及数量之比,则利用加权平均求出整体的平均值.
4.极差
定义 | 极差=最大值-最小值 |
意义 | 极差是用来反映一组数据变化范围的大小.我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围,用这种方法得到的差就称为极差. 极差仅只表示一组数据变化范围的大小,只对极端值较为敏感,而不能表示其它更多的意义. |
5.方差


6.标准差

【重要考向】
1.方差的概念
【思路】注意极差、方差、标准差的概念和区别,此外,当方差为0或1时,标准差跟方差相同.注意方差必须非负,而且方差为0时,每个数相同.
2.方差的计算
【思路】先计算平均值,再根据公式计算方差.
【2017.T4真题回顾】
3.方差的性质
【思路】

4.方差的大小比较
【思路】方差用来精确反应数据稳定性,方差越大数据越不稳定,方差越小数据越稳定.极差为一组数据最大值减去最小值,可粗略的反应一组数据稳定性.
温馨提示:文章由作者233网校-liuyun独立创作完成,未经著作权人同意禁止转载。