运用利率互换管理利率风险
运用利率互换管理利率风险相关课程
 运用利率互换管理利率风险考点解析
运用利率互换管理利率风险考点解析
 运用利率互换管理利率风险介绍
运用利率互换管理利率风险介绍
利用利率互换来转换资产或者负债的利率性质,管理资产或者负债中利率风险, 如固定利率的资产(或者负债)通过互换可以转换为浮动利率的资产(或者负债)。
利用利率互换来调整债务时,一般是为了使债务与利率敏感性资产相匹配、降低筹资成本,或者增加负债能力;
利用利率互换来调整资产时,一般是为了提高收益率。
(1)匹配资产和负债的利率风险
在2005年2月10日国家开发银行与中国光大银行进行了首笔人民币利率互换交易,名义本金为50亿元人民币,期限为10年。中国光大银行支付2.95%的固定利率,国开行支付浮动利率(1年期定期存款利率)。
国开行的资产主要为长期浮动利率贷款,负债以固定利率长期债券为主,资产和债务的期限结构不匹配,造成了很大的利率风险敞口。
通过利率互换,国开行填平了利率风险敞口,可以赚取稳定的利息差。
与此同时,中国光大银行的资产负债情况与国开行恰恰相反,其负债主要由短期存款构成,而资产主要是长期固定利率按揭贷款。通过利率互换,中国光大银行支付固定利率就可以与固定利率贷款相匹配,填平利率风险敞口。
(2)降低负债成本或者提高资产收益。结合利率环境的变化,可以灵活地通过利率互换降低负债成本。
假设某公司于2年前发行了7年期的固定利率债券,每年支付9.75%的利息。现实环境利率已经大幅下跌,公司现转换成浮动利率负债,以利用当前低利率的好处,公司根据当前市场报价签订了5年期每年以7.05%交换Libor的年度互换协议;通过互换,公司的融资成本变为Libor+2.7%(即9.75%-7.05%)的浮动利率,当时Libor为4.5%,故当年支付的息票率变为7.2%,比原来的9.75%节省了2.55个百分点。
运用利率互换管理利率风险考点试题
大咖讲解:运用利率互换管理利率风险

金融远期的定价
(一)远期价格
远期价格:使远期合约价值为零的交割价格。
远期合约签订时,如果信息是对称的,而且合约双方对未来的预期相同,那么合约双方所选择的交割价格应使合约的价值在签署合约时等于零,这意味着双方不需要交换任何现金流就可以处于远期合约的多头或空头状态。
远期价格不但可用于确定远期合约的交割价格,还可用于计算远期合约的价值,同时也是期货价格的参考。
e 为自然对数的底,
r 是无风险连续复利,
T 是远期合约的到期日。
Ft 是远期价格,
St 是股票当前的价格,
t 为当前时间,


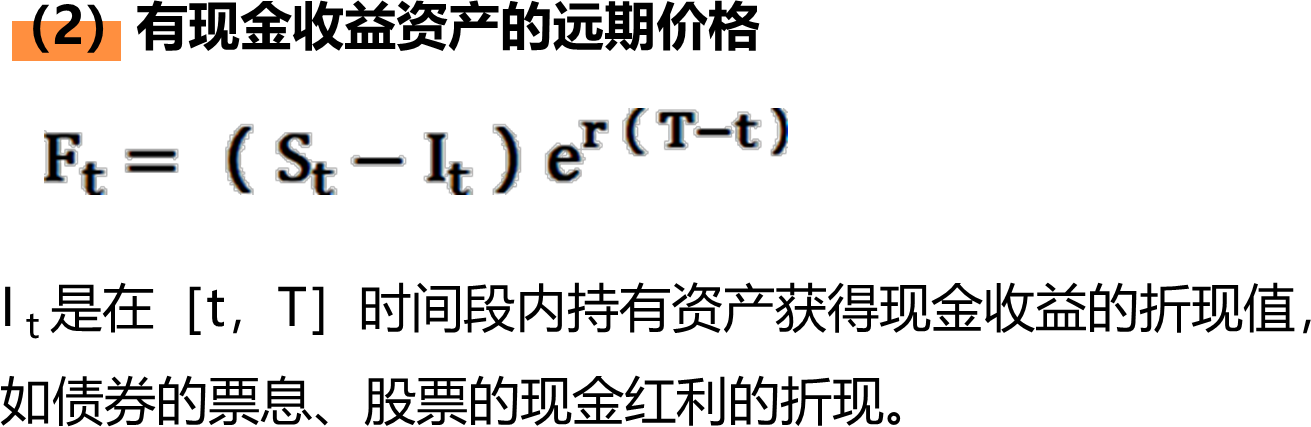
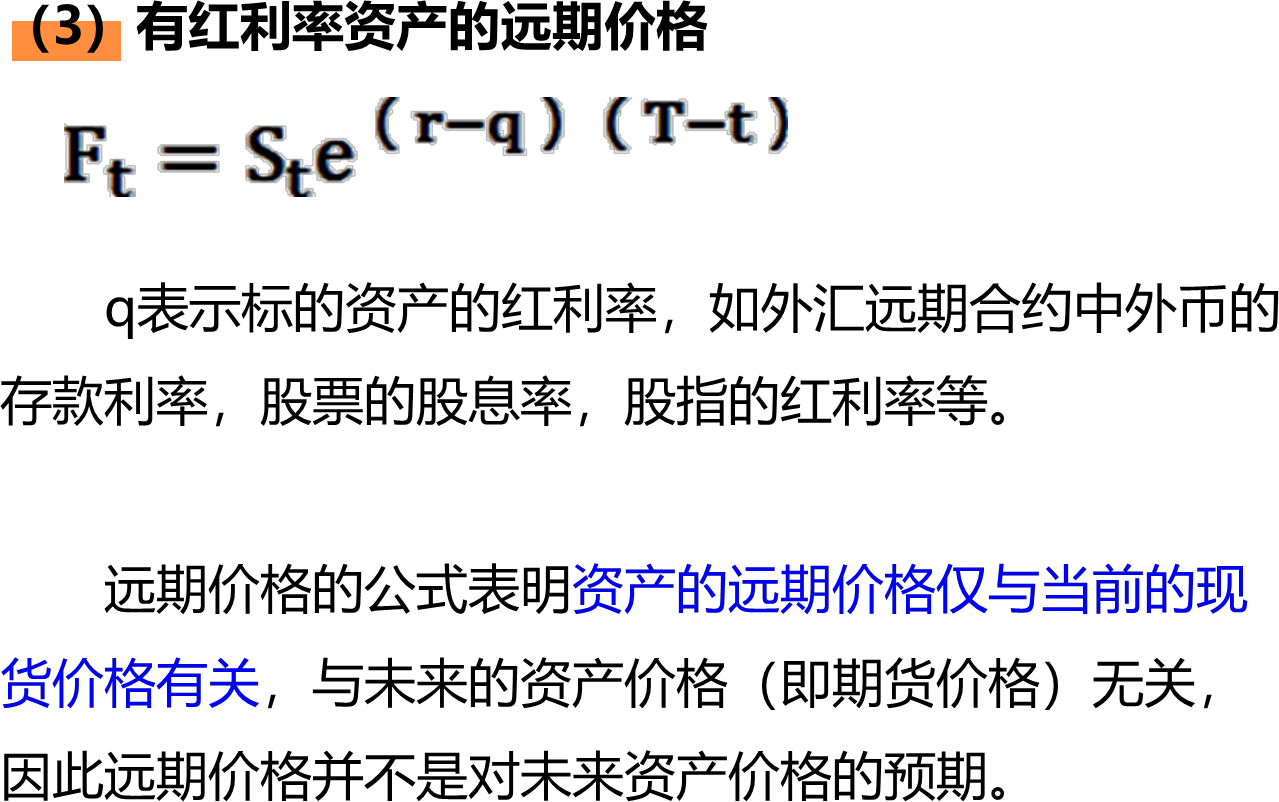
(二)远期合约的价值
远期合约的价值即买卖双方在交易远期合约时买方应该向卖方支付的现金,即产品本身的价值。
远期合约价值则是由远期交割价格与远期理论价格的价差决定的。
合约签署时,远期价格等于交割价格,此时合约价值为零。
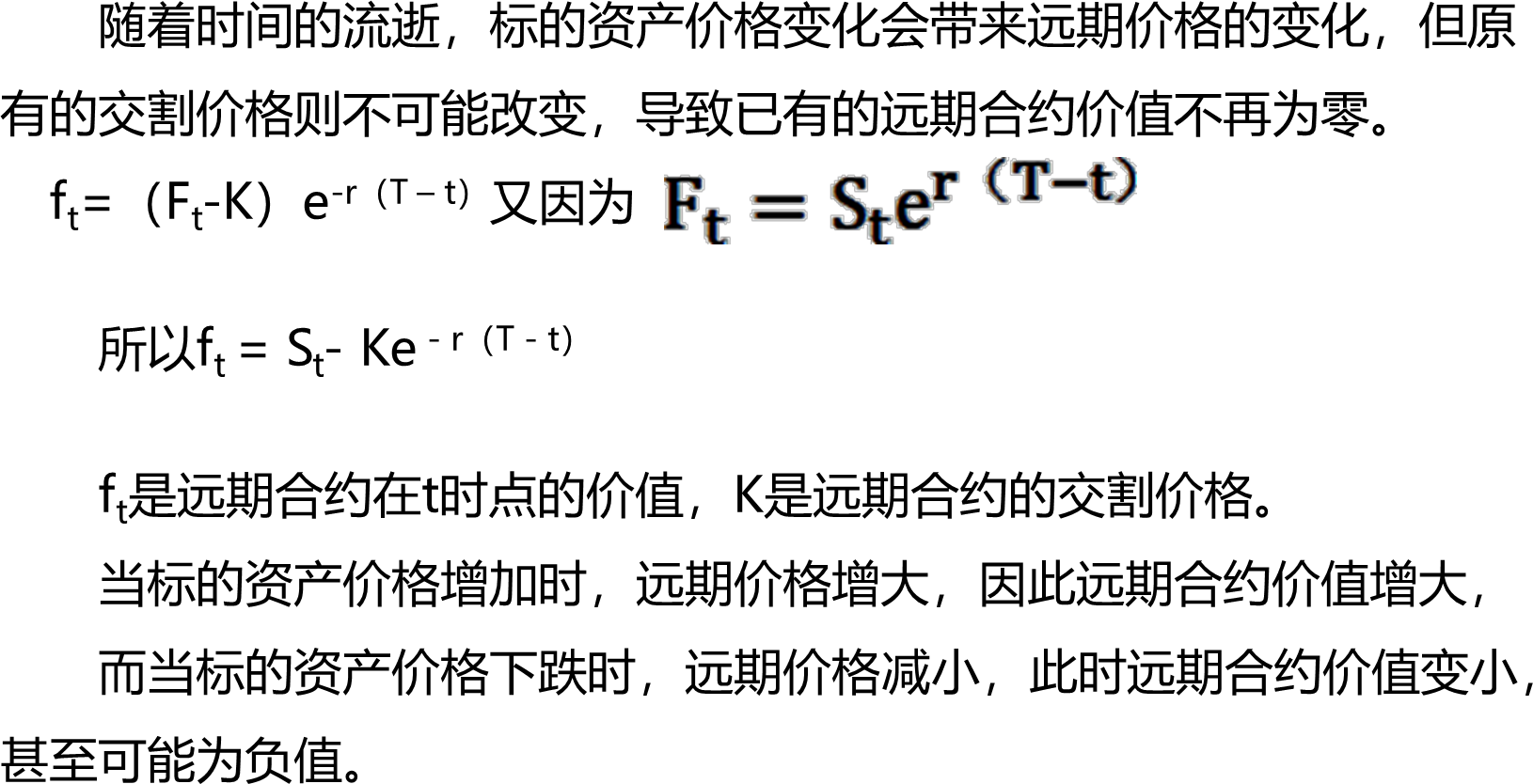
(三)远期利率协议的交割与估值
1远期利率协议的交割
远期利率协议(Forward Rate Agreements,FRA)是指买卖双方同意从未来某一时刻开始在后续的一定时期内按协议利率借贷一笔数额确定、以具体货币表示的名义本金的协议。
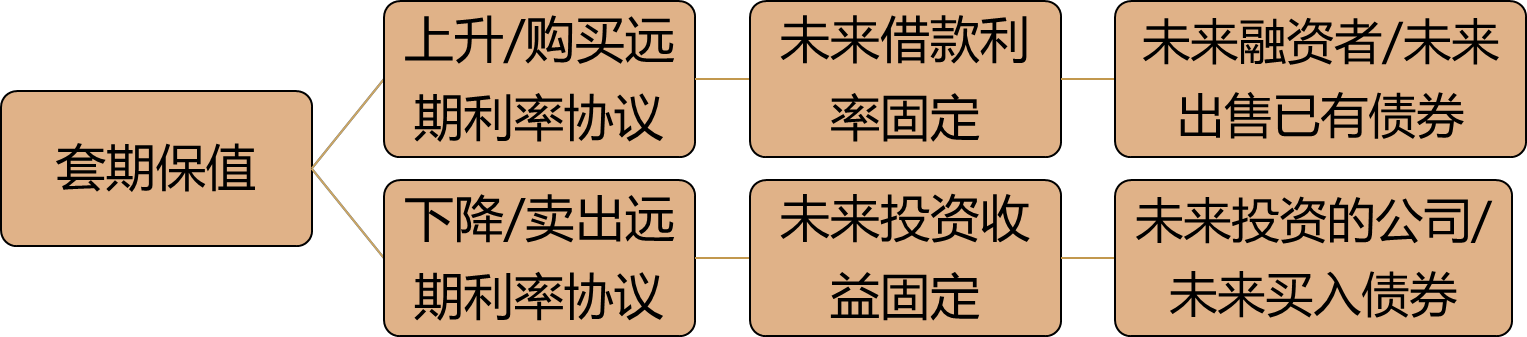
远期利率协议的买方是名义借款人,其订立远期利率协议的目的是规避利率上升的风险。
远期利率协议的卖方是名义贷款人,其订立远期利率协议的目的是规避利率下降的风险。
“名义”,是因为借贷双方不必交换本金,并不发生实际上的借贷行为,只是在交割日根据协议利率和参考利率之间的差额,交割利息差的折现值。
FRA中涉及三个时间点:
一个是协议生效日,
一个是名义贷款起息日,即交割日;
一个是名义贷款到期日,即到期日。
远期利率协议通常用交割日×到期日来表示,如,3×9的远期利率协议表示3个月之后开始的期限为6个月贷款的远期利率。

由于FRA的交割日是在名义贷款期初,不是在名义贷款期末,因此交割额的计算需要将利息差进行贴现,具体以FRA买方损益为例,
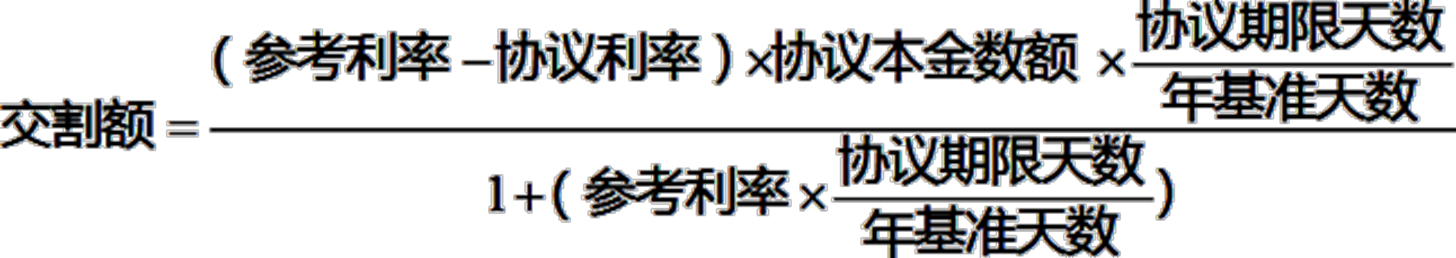
一般美元的年基准天数取360天,英镑的年基准天数取365天。
参考利率一般选取被广泛接受的市场利率,如美国是担保隔夜融资利率(SOFR)。
若参考(市场)利率>协议(约定)利率,交割额为正,卖方向买方支付交割额;
若参考利率<协议利率,交割额为负,买方向卖方支付交割额。
2远期利率协议的估值
远期利率协议与其他远期合约一样,在签订时理论价值为零,因此其协议利率等于远期利率(iF),计算公式为:
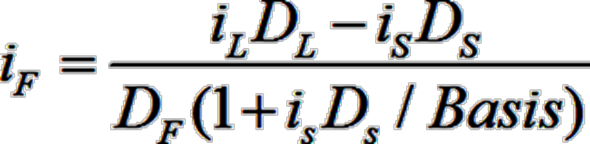
若期初协议利率不等于远期利率, 则可以通过构造套利策略获取无风险利润,在现实生活中,银行通常以远期利率为基准,将报出的买(卖)价格下浮(上浮)一定数量的基点。
(四)远期合约的套期保值
由于远期合约是由银行提供的场外交易产品,合约不规范,流动性较差,因此远期合约用于套期保值主要是静态套期保值。
在期初签订远期合约,后通过到期交割的方式完成套期保值,目的是完全消除套期保值期间价格波动的风险。
多头套期保值是买入远期合约的套期保值,空头套期保值指卖出远期合约的套期保值。
1. 基于远期利率协议的套期保值
某公司计划在3个月之后借入一笔为期6个月的1000万美元的浮动利率债务。根据该公司的信用状况,该公司能以6个月期的LIBOR利率水平借入资金,目前6个月期的LIBOR利率水平为6%,但该公司担心3个月后LIBOR将上升。
为此,它可以买入一份名义本金为1000万美元的3×9远期利率协议。假设现在银行挂出的3×9以LIBOR为参照利率的远期利率协议的报价为6.25%,那么该借款者就可以把借款利率锁定在6.25%的水平上。
2. 基于远期外汇合约的套期保值
多头套期保值就是通过买入远期外汇合约来避免汇率上升的风险,
它适用于在未来某日期将支出外汇的机构和个人,如进口商品、出国旅游、到期偿还外债、计划进行外汇投资等。
空头套期保值就是通过卖出远期外汇合约来避免汇率下降的风险,
它适用于在未来某日期将收到外汇的机构和个人,如:出口商品、提供劳务、现有的对外投资、到期收回贷款等。
当两种货币之间没有合适的远期合约时,套期保值者可利用第三种货币来进行交叉套期保值。

金融期货的定价
(一)金融期货的价格
金融期货主要包括股指期货、货币期货和利率期货等。
期货价格定义为使期货合约价值为零的理论交割价格。
由于期货是在场内进行的标准化交易,其逐日盯市制度、每日结清浮动盈亏的制度决定了期货在每日收盘后理论价值归为零, 即期货的报价相当于远期合约的协议价格,故期货的报价理论上等于标的资产的远期价格。
事实上由于交易制度的规定,理论报价在远期价格的基础上需要进行一定的调整。

(二)金融期货的套期保值
1 完全套期保值
类似远期合约,如果投资者希望套期保值的现货资产的种类和规模能够与市场上交易的期货的标的资产种类以及期货规模相匹配,可以进行类似远期合约的完全套期保值。
例如,一家美国公司想为2022年12月15日要支付的2500万欧元进行套期保值,已知12月份交割的欧元期货合约规模为12.5万欧元,则公司可以通过买入200份欧元期货合约进行完全套期保值。
在实际运用中,套期保值的效果会受到以下三个因素的影响:
• ①需要避险的资产与期货标的资产不完全一致;
• ②套期保值者不能确切地知道未来拟出售或购买资产的时间,因此不容易找到时间完全匹配的期货;
• ③需要避险的期限与避险工具的期限不一致。
在这些情况下,必须考虑基差风险、合约的选择和最优套期保值比率等问题。
2 基差风险与套期保值工具的选择
基差(Basis)=待保值资产的现货价格-用于保值的期货价格
如果打算进行套期保值的资产与期货的标的资产一致,在期货到期日时,期货价格将收敛到现货价格,因此基差会趋于0,但在到期日之前,基差可正可负。基差变动带来的风险称之为基差风险。
为了降低基差风险,要选择合适的期货合约,它包括两个方面:
• ①选择合适的标的资产;
• ②选择合约的交割月份。
选择标的资产的标准是标的资产价格与保值资产价格的相关性。
相关性越好,基差风险就越小。
因此选择标的资产时,最好选择保值资产本身,若保值资产没有期货合约,则选择与保值资产价格相关性最好的资产的期货合约。
在选择合约的交割月份时,要考虑是否打算实物交割。对于大多数金融期货而言,实物交割的成本并不高,在这种情况下,通常应尽量选择与套期保值到期日相一致的交割月份,从而使基差风险最小。
若套期保值者不能确切地知道套期保值的到期日,也应选择交割月份靠后的期货合约。
3 最优套期保值比率的确定
套期保值比率是指期货合约的总价值与套期保值资产现货总价值之间的比率,即一单位现货头寸保值者所建立的期货合约单位。
若QF表示一份期货合约的价格,N表示期货的份数, NS表示待保值资产的价值,则:

当套期保值资产价格与标的资产的期货价格相关系数等于1时,为了使套期保值后的风险最小,套期保值比率应等于1。
而当相关系数不等于1时,套期保值比率就可能不等于1。
(1)最优套期保值比率的理解。
无论多头套期保值还是空头套期保值,都有:
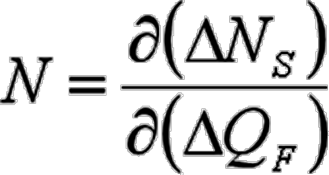
• 这个公式体现了期货最优套期保值比率的本质含义:期货到期时,期货价格每变动1单位时,被套期保值的现货价格变动的量就是最优套期保值比率应确定的期货份数。反过来也就意味着1单位的现货需要N单位的期货头寸对其进行套期保值,才能达到最优的消除风险的效果。
(2)货币期货的最优套期保值比率
货币期货的套期保值方向选择与外汇远期是相同的,当面临外币汇率上升带来的损失时,可以买入该外币的期货;相反则卖出该外币的期货。
到目前为止,学术界和实务界已经提出了多种估计最优套期保值比率的方法,最常见也比较具有一般性的是“最小方差套期保值比率”,即套期保值的目标是使得整个套期保值组合收益的波动最小化的套期保值比率,具体体现为套期保值收益的方差最小化。
货币期货在方差最小的情况下,其最优套期保值比率为:
用上述比率配置外汇期货进行套期保值,可以使组合价值变动最小,即在方差意义下风险最小,此时期货的最佳数量为:
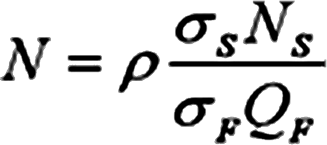
(3)股指期货最佳套期保值数量
当用股指期货为股票组合套期保值时,股指期货最佳套期保值数量(N)为:
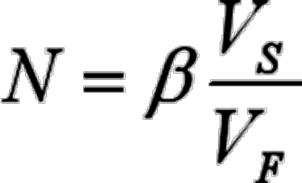
其中,Vs 为股票组合的价值;VF为单位股指期货合约的价值(等于期货价格乘以合约大小);β为该股票组合的β值。因为股票组合没有单位价格,因此很少使用套期保值比率,直接计算套期保值需要的期货数量即可。
某公司打算运用6个月期的S&P500股价指数期货为其价值500万美元的股票组合套期保值,该组合的β值为1.8,当时的期货价格为400。由于一份该期货合约的价值为400×500=20万美元,因此该公司应卖出的期货合约的数量为:

(4)利率期货与久期套期保值
利用利率期货进行套期保值方向与远期利率协议是完全相反的,因为利率期货以债券或者短期存款为标的,当利率上升时,债券价格或者短期存款的价格是下跌的。因此投资者担心利率上升带来的损失时,要卖出利率期货,这样当利率上升时,利率期货价格下跌,利率期货空头可以获益,用以弥补利率上升带来的损失。相反,当投资者担心利率下降带来的损失时,要买入利率期货。
由于当市场利率变动时,债券价格的变动幅度取决于该债券的久期,而利率期货价格的变动幅度也取决于利率期货标的债券的久期,因此我们可以根据保值债券与标的债券的久期来计算套期保值比率。
令S和DS分别表示需进行套期保值资产的价格和久期,F表示利率期货的价格,DF表示期货合约标的债券的久期。则为了对冲收益率变动对保值债券价值的影响,所需要的期货合约数(N)为:
2023年11月20日,某基金管理者持有2000万美元的美国政府债券,他担心市场利率在未来6个月内将剧烈波动,因此他希望卖空2024年6月到期的长期国债期货合约,假设国债的面值为 100 美元,一份国债期货合约对应于1000 份国债,即一份国债期货对应于10万美元的国债。该合约目前市价为94.1875美元,那么每份合约价值94187.50美元。假设需保值的债券平均久期为8年,长期国债期货合约的平均久期为10.3年。则为进行套期保值,他应卖空的期货合约数为:
注意:基于久期的套期保值是不完美的,存在着较多的局限性,它没有考虑债券价格与收益率关系曲线的凸度问题,而且它是建立在收益率曲线平移的假定上,因此在实际运用时要多加注意。
4 滚动套期保值
由于期货合约的有效期通常不超过1年,而套期保值的期限有时又长于1年,在这种情况下,就必须采取滚动的套期保值策略,即建立一个期货头寸,待这个期货合约到期前将其平仓,再建立另一个到期日较晚的期货头寸直至套期保值期限届满。如果交易者通过几次平仓才实现最终的套期保值目的,则交易者将面临几个基差风险。
(三)金融期货的套利
金融期货可以利用基差的变动规律进行:
期现套利(现货与期货反向操作进行套利的方式,利率期货和股指期货市场应用较多)
跨期套利(在同一期货品种不同期限的期货间进行)
跨市场套利(在外汇期货市场进行)。
1 期现套利
它是利用期货价格与标的资产现货价格的差异进行套利的交易,即在现货市场买入(卖出)现货的同时,按同一标的资产,以同样的规模在期货市场上卖出(买入)该资产的某种期货合约,并在未来一段时间后同时平仓的交易。
由于期货价格理论近似于远期价格,而远期价格又决定于标的资产的现货价格,因此期货价格与现货价格存在着强相关性,当期货价格与现货价格偏离超过理论差距时就会产生套利机会,可以通过期货和现货方向相反、头寸相同的方式进行套利。
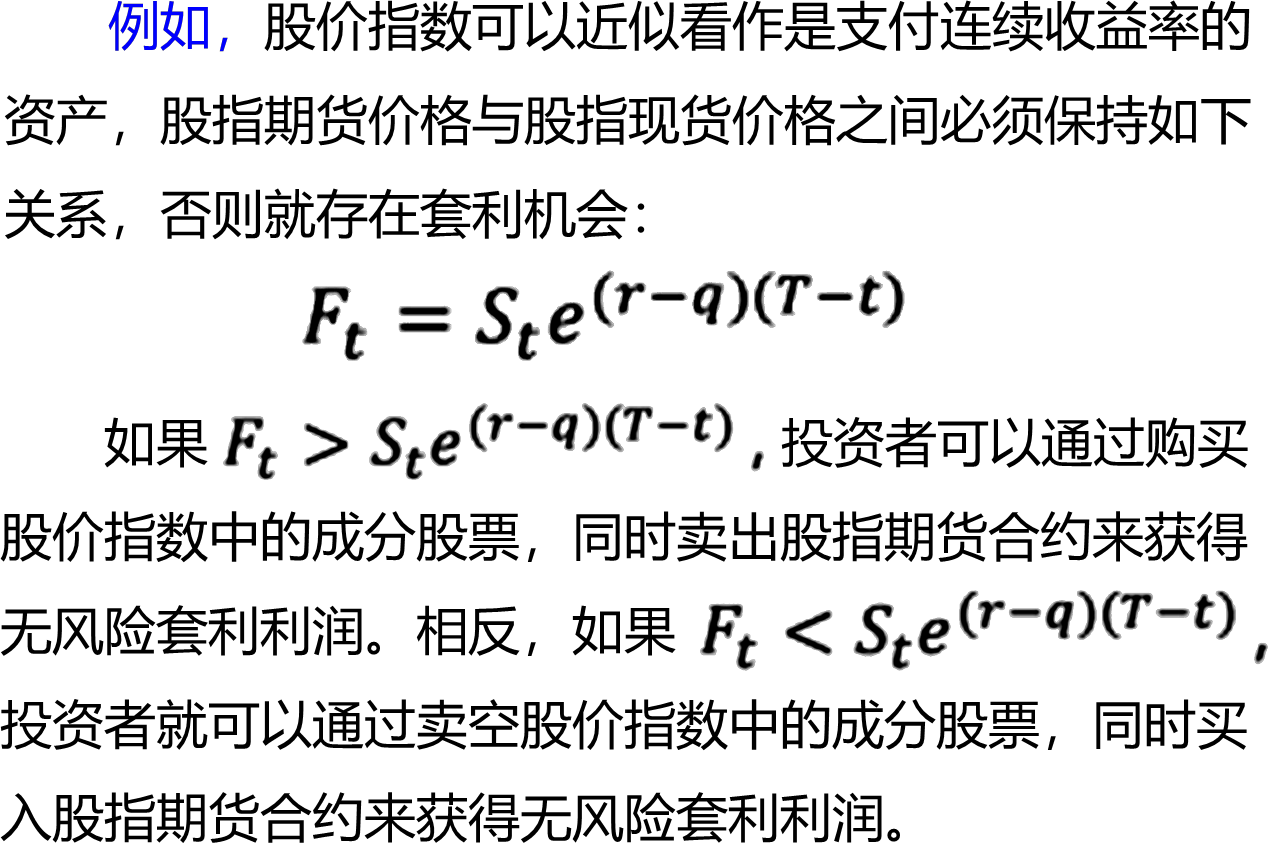
2 跨期套利
跨期套利是指在同一期货市场(如股指期货)的不同到期期限的期货合约之间进行的套利交易,
具体来说,就是买入(卖出)某一较短期限的期货合约的同时, 卖出(买入)另一相同标的资产的较长期限的期货合约,在较短期限的期货合约到期时或到期前同时将两个期货合约对冲平仓的交易。
跨期套利在同一市场进行,且期货市场没有卖空限制,因此跨期套利是套利交易中使用较多的策略。
跨期套利依赖的指标就是基差,当基于同一标的资产的不同期限的期货合约报价产生的基差差异超出正常范围时,可以通过跨期套利获取无风险利润。
3 跨市场套利
跨市场套利是指利用同一种期货合约在不同交易所之间的价差而进行的套利交易。
具体来说,就是在买入(卖出)某一交易所的某一期货合约的同时,按同一数量、同一到期期限卖出(买入)另一交易所的同一期货合约,并在未来某一时间同时将两种期货合约对冲平仓的交易。
货币期货中使用较多。

互换的定价
(一)利率互换的定价
利率互换是指买卖双方同意在未来的一定期限内根据同种货币的同样的名义本金交换现金流。
其中一方的现金流根据浮动利率计算,而另一方的现金流根据固定利率计算,
通常双方只交换利息差,不交换本金。
互换的期限通常在1年以上,有时甚至在15年以上。
普通利率互换可以由一组远期利率协议复制,也可以由固定利率债券和浮动利率债券的组合复制,因此利率互换的价值等于债券组合的价值,可以运用债券组合对互换进行定价。
以利率互换的买方为例,利率互换的买方支付固定利率,获得浮动利率,因此可以将买方的收益等价于其发行了一个固定利率的债券,购买了一个浮动利率的债券,故其价值为:
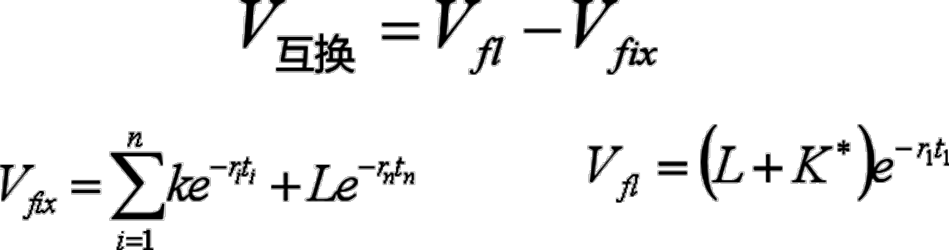
(二)货币互换的定价
货币互换是买卖双方将一种货币的本金和利息与另一种货币的本金和利息进行交换的协议。
货币互换的买方在期初获得外币,并将等值的本币借给卖方;
在合约期限内买方支付外币利息,获取本币利息;
合约到期时买方向卖方偿还外币本金,同时获得本币的本金。
由此可见,货币互换与利率互换在结构和运作机制上相似,但它们是两种不同的互换合约,其主要不同在于以下三个方面。
• (1)利率互换只涉及一种货币,而货币互换要涉及两种货币。
• (2)在协议开始和到期时,货币互换双方常常交换本金,而利率互换不涉及本金的交换。
• (3)货币互换双方的利息支付可以均为固定利率,也可以均为浮动利率,或者固定利率与浮动利率互换,而标准利率互换多见于固定利率与浮动利率互换。
定义V互换为货币互换买方的价值,那么:
V互换=BD-S0BF
BF 是用外币表示的从互换中分解出来的外币债券的价值;
BD是从互换中分解出来的本币债券的价值;
S0是即期汇率(外币兑本币,如人民币为本币,美元为外币,1美元=6.2人民币元,则S0 =6.2)。
对于付出本币利息,收入外币利息的那一方。即卖方,即价值为: -V互换= S0BF-BD
(三)金融互换的套利
金融互换的套利运用的是比较优势原理。
|
英国 |
法国 |
|
|
产能 |
小麦 8份/天 |
小麦 3份/天 |
|
鱼 4份/天 |
鱼 3份/天 |
|
|
单独工作2天(无合作) |
小麦11份,鱼7份 |
|
|
合作2天 |
小麦16份,鱼6份 |
|
互换是比较优势理论在金融领域最生动的运用。根据比较优势理论,只要满足以下两种条件,就可以通过互换进行套利:
① 双方对对方的资产或负债均有需求;
② 双方在两种资产或负债上存在比较优势。
1 利率互换的套利
假设A、B公司都想借入5年期的1000万美元借款,A公司想借入与6个月期相关的浮动利率借款,B公司想借入固定利率借款。但两家公司信用等级不同,故市场向它们提供的利率也不同。
|
表8-4 市场提供给A、B两家公司的借款利率 |
|
固定利率 浮动利率 |
|
A公司 6.00% 6个月期 Libor+0.30% |
|
B公司 7.20% 6个月期 Libor+1.00% |
|
注:表中的利率均为一年计一次复利的年利率。 |
A公司 6.00%, Libor+0.30%
B公司 7.20%, Libor+1.00%
A公司在固定利率市场上存在比较优势,7.20%-6.00%=1.2%
B公司在浮动利率市场上存在比较优势,
(Libor+1.00%)-(Libor+0.30%)=0.7%
套利利润= 1.2%-0.7%= 0.5%
A公司和B公司可以通过如下互换分享无风险利润,降低双方的融资成本:

A 、B 两家公司通过利率互换套利如图8-7所示。

A 公司融资成本Libor + 6% - 6% = Libor ,(浮动);
B 公司融资成本6% + Libor + 1% - Libor = 7% ,(固定)。
互换前:
A公司 6.00%, Libor+0.30%
B公司 7.20%, Libor+1.00%
互换后:
A 公司节约成本Libor + 0.3% - Libor = 0.3% ,
B 公司节约成本7.2% -7% = 0 .2% ,
A 、B 公司通过利率互换分别获利0 .3% 和0. 2%。
2 货币互换的套利
假设英镑和美元汇率为1英镑 =1.5 美元。
A公司想借入5年期的1000 万英镑借款,
B公司想借入5年期的1500 万美元借款。
|
表8-5 市场向A、B两家公司提供的借款利率 |
||
|
美元 |
英镑 |
|
|
A公司 |
8.00% |
11.6% |
|
B公司 |
10.00% |
12% |
|
A- B |
-2% |
-0.40% |
A公司 $8.00%, £11.6%
B公司 $10.00%, £12.00%
A公司在美元市场上存在比较优势,10.00%-8.00%=2.00%
B公司在英镑市场上存在比较优势, 12.00%- 11.6%=0.4%
套利利润= 2.00%-0.4%= 1.6%
A公司在货币互换中支付英镑利息,获得美元利息,同时在市场上借入美元借款;
B公司在货币互换中支付美元利息,获得英镑利息,同时在市场上借入英镑借款。

互换前:
A公司 $8.00%, £11.6%
B公司 $10.00%, £12.00%
互换后:
A公司融资英镑的成本为8%+10.8%-8%=10.8%;
B公司融资美元成本为8%+12%-10.8%=9.2%,
A公司、B公司均节约了0.8%的成本。
总结:
1、对外,买自己有比较优势的;
2、对内,支付对方自己想要的;
3、分利,有说明按说明,无说明,双方平分。


(四)运用利率互换管理利率风险
利用利率互换来转换资产或者负债的利率性质,管理资产或者负债中利率风险, 如固定利率的资产(或者负债)通过互换可以转换为浮动利率的资产(或者负债)。
利用利率互换来调整债务时,一般是为了使债务与利率敏感性资产相匹配、降低筹资成本,或者增加负债能力;
利用利率互换来调整资产时,一般是为了提高收益率。
(1)匹配资产和负债的利率风险
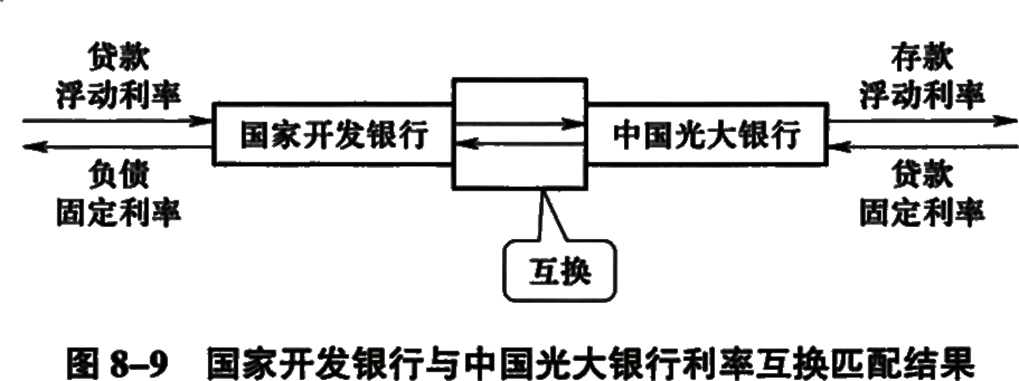
在2005年2月10日国家开发银行与中国光大银行进行了首笔人民币利率互换交易,名义本金为50亿元人民币,期限为10年。中国光大银行支付2.95%的固定利率,国开行支付浮动利率(1年期定期存款利率)。
国开行的资产主要为长期浮动利率贷款,负债以固定利率长期债券为主,资产和债务的期限结构不匹配,造成了很大的利率风险敞口。
通过利率互换,国开行填平了利率风险敞口,可以赚取稳定的利息差。
与此同时,中国光大银行的资产负债情况与国开行恰恰相反,其负债主要由短期存款构成,而资产主要是长期固定利率按揭贷款。通过利率互换,中国光大银行支付固定利率就可以与固定利率贷款相匹配,填平利率风险敞口。

(2)降低负债成本或者提高资产收益。结合利率环境的变化,可以灵活地通过利率互换降低负债成本。
假设某公司于2年前发行了7年期的固定利率债券,每年支付9.75%的利息。现实环境利率已经大幅下跌,公司现转换成浮动利率负债,以利用当前低利率的好处,公司根据当前市场报价签订了5年期每年以7.05%交换Libor的年度互换协议;通过互换,公司的融资成本变为Libor+2.7%(即9.75%-7.05%)的浮动利率,当时Libor为4.5%,故当年支付的息票率变为7.2%,比原来的9.75%节省了2.55个百分点。
(五)运用货币互换管理汇率风险
货币互换可以用来转换资产或债务组合的货币构成,在全球各市场之间进行套利,从而一方面降低筹资者的融资成本或提高投资者的资产收益,另一方面促进全球金融市场的一体化。

期权的定价
(一)金融期权的价值结构
期权费也可称为期权价格、期权的权利金,指的是期权交易中的价格,即购买期权的一方为自己获得的买入标的资产或卖出标的资产的权利预先支付给期权卖方的费用。
期权费由两部分构成:内在价值和时间价值。
1 内在价值
内在价值指期权按执行价格立即行使时所具有的价值, 一般大于0。
看涨期权,内在价值相当于标的资产现价与执行价格的差;
看跌期权,内在价值相当于执行价格与标的资产现价的差。
2 时间价值
时间价值指的是期权费减去内在价值部分以后的余值。
在实务中,所有期权的出售方都无一例外地要求买方支付的期权费高于期权的内在价值。
原因:期权的非对称性表明期权卖方具有亏损的无限性和盈利的有限性特征,需要对卖方所承担的风险予以补偿。
期限越长的期权,基础资产价格发生变化的可能性越大,因而期权的时间价值越大。
在执行价格既定时,期权费大小与期权的期限长短呈正相关关系。
期权越临近到期日,时间价值就越小,这种现象被称为时间价值衰减。
当期权临近到期日时,在其他条件不变的情况下,其时间价值下降速度加快,并逐渐趋向于0, 一旦到达到期日,期权的时间价值将为0。
(二)金融期权价格的合理范围
1. 欧式看涨期权价格的合理范围
由于看涨期权赋予的是买入标的资产的权利,因此其价格不会超过标的资产自身的价格,否则,套利者可以通过购买标的资产并出售买权,轻易获得无风险利润。
同时由于期权时间价值是非负的,因此其价格也不会低于内在价值,故欧式看涨期权的期权费收值的合理范围为:
ma× [St - Xe –r(T-t), 0 ]≤C ≤ St
St 为标的资产的现价;X 为期权的执行价格;
e 为自然对数的底;r为无风险利率;t为当前时间;T为期权到期时间;c为欧式看涨期权的期权费。
由于欧式期权不能提前执行,因此,其内在价值通过折现进行了调整。
2. 欧式看跌期权价格的合理范围
由于看跌期权赋予的是以固定价格X卖出标的资产的权利, X 是执行看跌期权带来的最高收益,故看跌期权的价格应低于执行价格,而欧式看跌期权无法提前执行,因此其价格要低于最高收益的折现值; 否则, 套利者可以通过出售卖权并将所得收入以无风险利率进行投资,获得无风险收益。
同时,看跌期权的时间价值也是非负的,故其期权费也不会低于其内在价值。
综合上述分析,欧式看跌期权的期权费取值的合理范围为:
ma× [Xe –r(T-t)-St , 0 ]≤p ≤ Xe –r(T-t)
P为欧式看跌期权的期权费。
3. 美式看涨期权价格的合理范围
在标的资产没有红利支付时, 美式看涨期权虽然可以提前执行,但提前执行获得的资产不产生红利,而货币可以产生时间价值,因此提前执行美式看涨期权是不合理的,其价值的合理范围与欧式看涨期权相同。
不过当标的资产有红利或者利息支付时, 美式看涨期权是可能提前执行的。
4. 美式看跌期权价格的合理范围
由于提前执行看跌期权相当于提前卖出资产,获得现金,而现金可以产生无风险收益,因此直观上看, 美式看跌期权可能提前执行,故美式看跌期权的价格通常大于欧式看跌期权,而其取值范围也相应扩大为:
ma× (X -St ,0 )≤p ≤ X
否则,套利者可以以低于期权内在价值的价格购入期权,然后马上行使期权来获得无风险利润。
p 为美式看跌期权的期权费。
(三)金融期权的套期保值
1. 利用期权为现货资产套期保值
当未来需要买入现货资产,但却担心未来价格上涨增加购买成本时,可以买入看涨期权进行套期保值;
当未来需要卖出现货资产,但却担心未来价格下跌降低资产收益时,可以买入看跌期权进行套期保值。
2. 期权的动态套期保值
由于金融期权合约到期损益的不对称性,期权价格与其影响因素之间产生了非线性关系,因此如果投资者的资产组合中包含了售出的期权,为了控制无限的亏损可能,需要对期权产品进行动态套期保值,当影响因素如标的资产价格发生变化时需要及时调整标的资产的头寸,以达到更好的套期保值的目的。
影响期权价格的因素主要包括:标的资产价格、标的资产的波动率、无风险利率、到期期限、执行价格五个因素,除执行价格外其他因素都是变动的,故期权套期保值需要考虑各个因素的变动。
期权的套期保值也被称为希腊字母套期保值。
(四)金融期权的套利
1. 看涨期权与看跌期权之间的套利
看涨和看跌期权合理的价格范围可知,当看涨期权和看跌期权价格在上述价格范围之外时,就会存在套利机会,可以通过买卖标的资产和期权设计套利策略赚取无风险利润。
相同标的资产、相同到期日以及相同执行价格的欧式看涨期权和l欧式看跌期权之间还应该满足平价关系:
c + Xe –r(T-t)= St +p
如果不能满足上述等式,就可以设计套利策略获取无风险利润。
假设某投资者认为某一股票的价格在以后的3个月中将发生重大变化,该股票的现行市场价值为69美元,该投资者可以通过同时购买到期期限为3个月,执行价格为70美元的一个看涨期权和一个看跌期权来进行套利。假定看涨期权的成本为4美元,看跌期权的成本为3美元。如果到期时股票价格保持69美元不变,则该策略的成本为6美元(初始投资7美元,此时看涨期权到期价值为0,看跌期权到期价值为1美元)。如果到期时股票价格为70美元,则会有7美元的损失(这是可能发生的最坏情况)。但是,如果股票价格跳跃到90美元,则该策略可获利13美元;如果股票价格跌到55美元,可获利8美元。
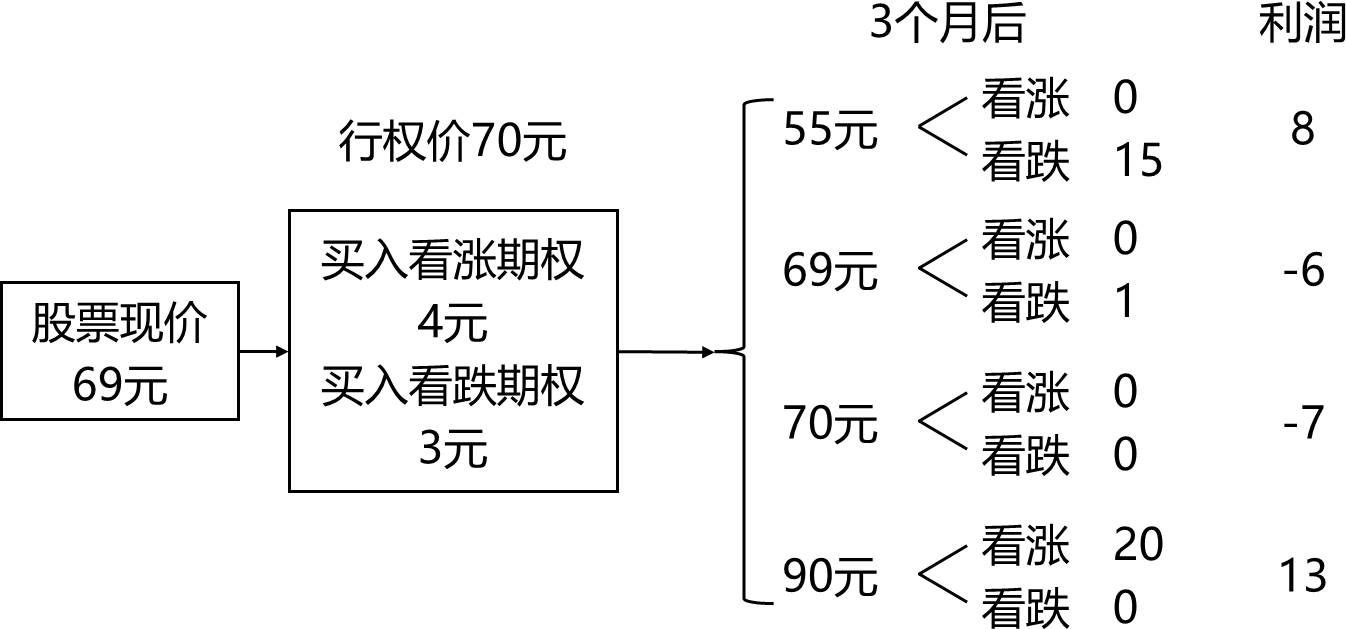
2. 垂直价差套利
相同标的资产、相同期限、不同协议价格的看涨期权的价格或看跌期权的价格之间存在一定的不等关系, 一旦在市场交易中存在合理的不等关系被打破,则存在套利机会,这种套利被称为垂直价差套利,包括蝶式价差套利、盒式价差套利、鹰式价差套利等。
以蝶式价差套利为例。
考虑三种协议价格X1 、X2 和X3,相同标的资产, 相同到期日的看涨期权,X2 =(X1 + X3)÷ 2 ,利用套利定价原理可以推导出三者的期权应该满足: 2C2 < C1 +C3, 当该关系不满足时,可以通过买入执行价格为X1和X3的期权,卖出执行价格为X2的期权进行套利。
假定某一股票的现价为61美元,如果某个投资者认为这以后的6个月中股票价格不可能发生重大变化。假定6个月期看涨期权的市场价格见表:
|
执行价格(美元) |
看涨期权的价格(美元) |
|
55 |
10 |
|
60 |
7 |
|
65 |
5 |
通过购买一个执行价格为55美元的看涨期权,购买一个执行价格为65美元的看涨期权,同时出售两个执行价格为60美元的看涨期权,投资者就可以构造一个蝶式价差期权。
构造这个期权组合的成本为10+5 -(2×7)=1美元。
|
执行价格(美元) |
看涨期权的价格(美元) |
操作 |
|
55 |
10 |
购买1份(-10) |
|
60 |
7 |
卖出2份(2×7) |
|
65 |
5 |
购买1份(-5) |
如果在6个月后,股票价格高于65美元或低于55美元,该策略的收益为0,投资者的净损失为1美元。
如果股票价格在56〜64美元之间,运用该策略就可以获利。当6个月后股票价格为60美元时,会得到最大利润4美元。
|
执行价格及方向 |
到期日价格<55 |
56 |
60 |
64 |
到期日价格>65 |
|
买入看涨(55)1份 |
0 |
1 |
5 |
9 |
15 |
|
卖出看涨(60)2份 |
0 |
0 |
0 |
-8 |
-20 |
|
买入看涨(65)1份 |
0 |
0 |
0 |
0 |
5 |
3. 水平价差套利
水平价差套利是利用相同标的资产、相同协议价格、不同期限的看涨期权或看跌期权价格之间的差异来赚取无风险利润。
一般说来,虽然欧式期权只能在有效期结束时执行,但期限较长的期权价格仍应高于期限较短的期权;否则就存在无风险套利机会。
典型的如日历价差交易策略,即买入期限较长的期权,同时卖出期限较短具有相同标的资产、相同行使价格的期权进行套利。
4. 波动率交易套利
标的资产的波动率是期权定价中最难以确定的因素,如果知道期权的价格,通过期权定价公式反向求解,可以计算出标的资产的一个波动率,称为期权的隐含波动率。
隐含波动率过高则意味着期权相对昂贵,如果过低,期权就会相对便宜。
由于波动率具有可预测性,因此可以通过预测波动率与隐含波动率的比较确定期权价值的涨跌,
如预测波动率高于隐含波动率,则未来期权价值应该增加,反之应该降低。
由于看涨期权和看跌期权价值均与波动率正相关,且相同执行价格的看涨、看跌期权的隐含波动率应该相等。 因此一般可以通过看涨和看跌期权的组合进行套利,即跨式组合套利。
预测>隐含,买入看涨期权和看跌期权,即跨式组合多头套利;否则,可以通过卖出看涨期权和看跌期权进行套利,即跨式组合空头套利。

远期价格
远期价格:使远期合约价值为零的交割价格。
远期合约签订时,如果信息是对称的,而且合约双方对未来的预期相同,那么合约双方所选择的交割价格应使合约的价值在签署合约时等于零,这意味着双方不需要交换任何现金流就可以处于远期合约的多头或空头状态。
远期价格不但可用于确定远期合约的交割价格,还可用于计算远期合约的价值,同时也是期货价格的参考。
e 为自然对数的底,
r 是无风险连续复利,
T 是远期合约的到期日。
Ft 是远期价格,
St 是股票当前的价格,
t 为当前时间,


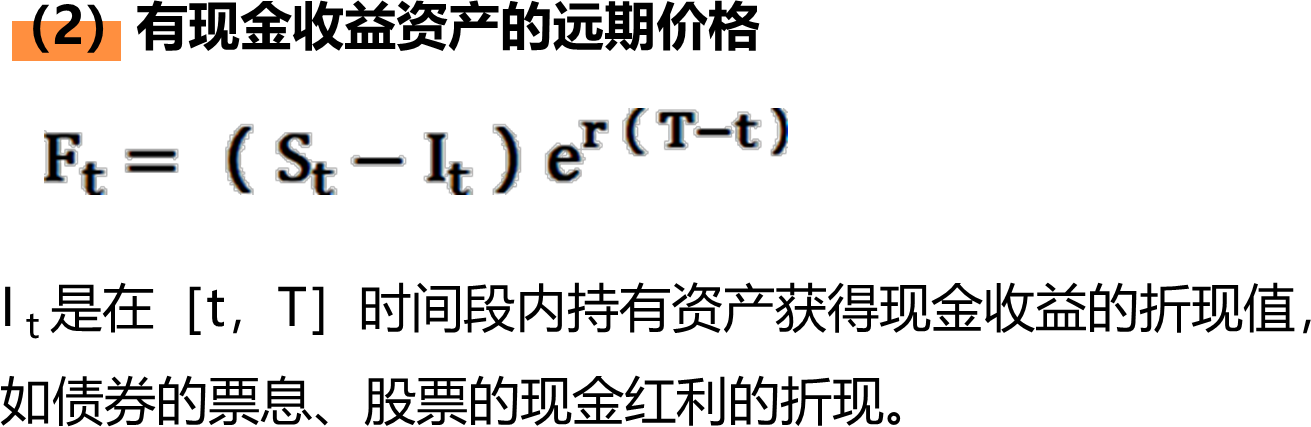
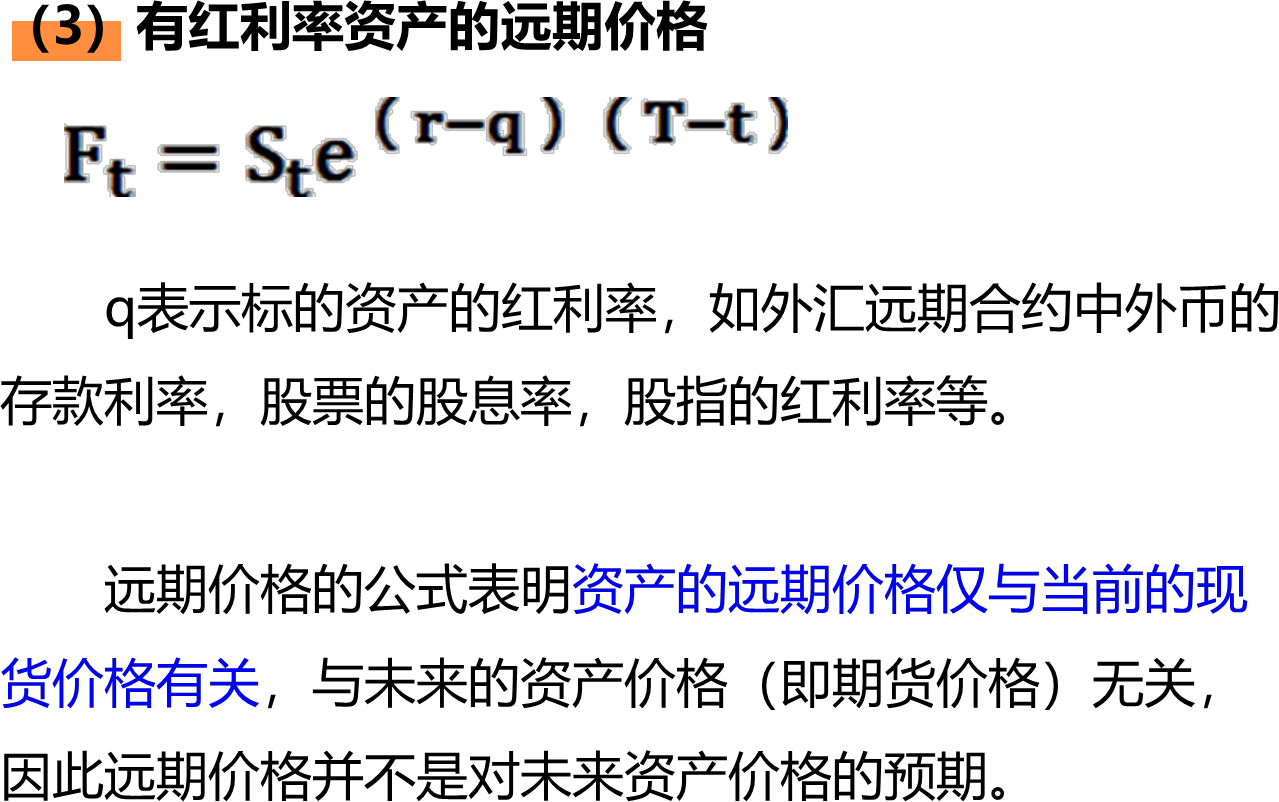

远期合约的价值
远期合约的价值即买卖双方在交易远期合约时买方应该向卖方支付的现金,即产品本身的价值。
远期合约价值则是由远期交割价格与远期理论价格的价差决定的。
合约签署时,远期价格等于交割价格,此时合约价值为零。
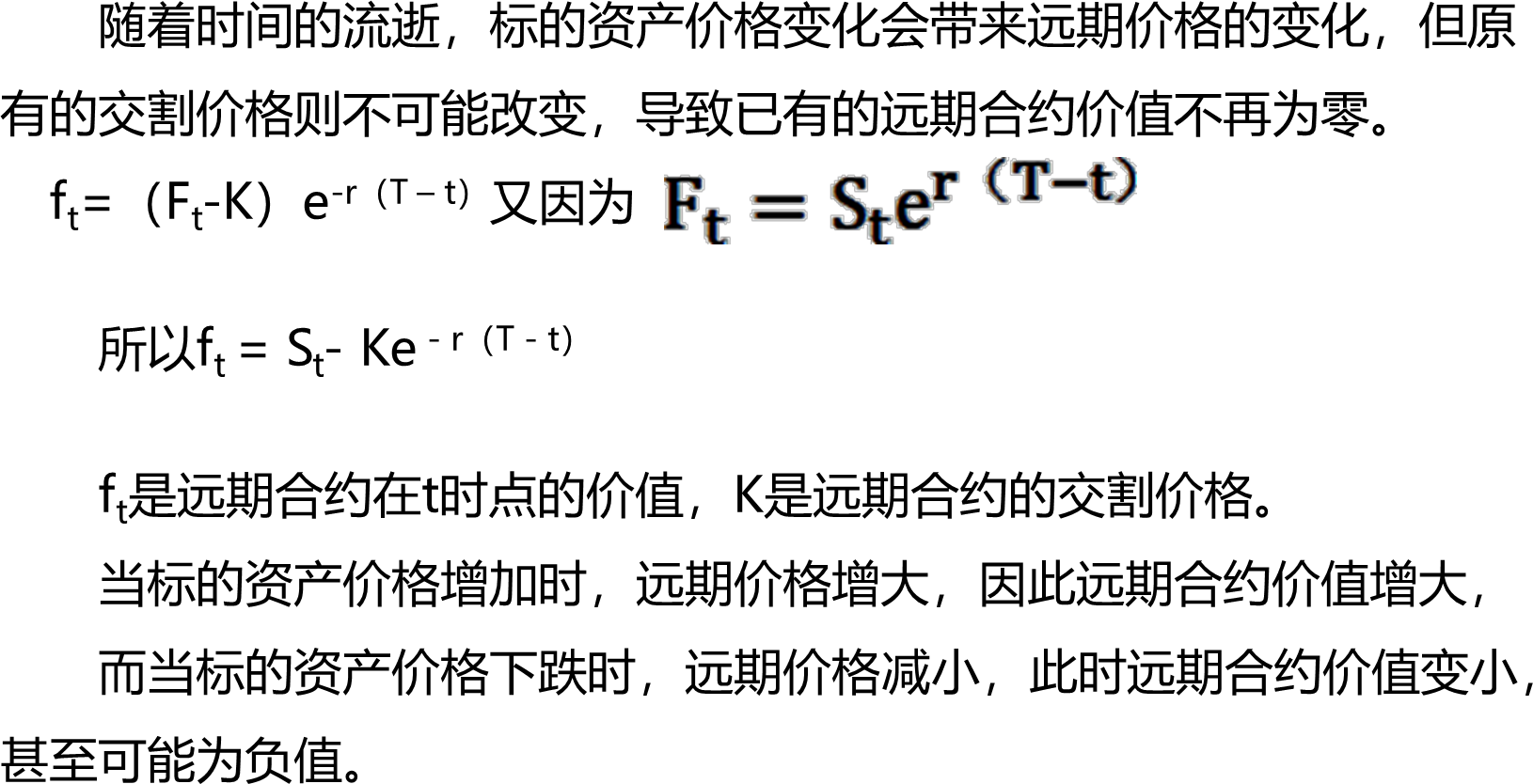

远期利率协议的交割与估值
1远期利率协议的交割
远期利率协议(Forward Rate Agreements,FRA)是指买卖双方同意从未来某一时刻开始在后续的一定时期内按协议利率借贷一笔数额确定、以具体货币表示的名义本金的协议。
远期利率协议的买方是名义借款人,其订立远期利率协议的目的是规避利率上升的风险。
远期利率协议的卖方是名义贷款人,其订立远期利率协议的目的是规避利率下降的风险。
“名义”,是因为借贷双方不必交换本金,并不发生实际上的借贷行为,只是在交割日根据协议利率和参考利率之间的差额,交割利息差的折现值。
FRA中涉及三个时间点:
一个是协议生效日,
一个是名义贷款起息日,即交割日;
一个是名义贷款到期日,即到期日。
远期利率协议通常用交割日×到期日来表示,如,3×9的远期利率协议表示3个月之后开始的期限为6个月贷款的远期利率。

由于FRA的交割日是在名义贷款期初,不是在名义贷款期末,因此交割额的计算需要将利息差进行贴现,具体以FRA买方损益为例,
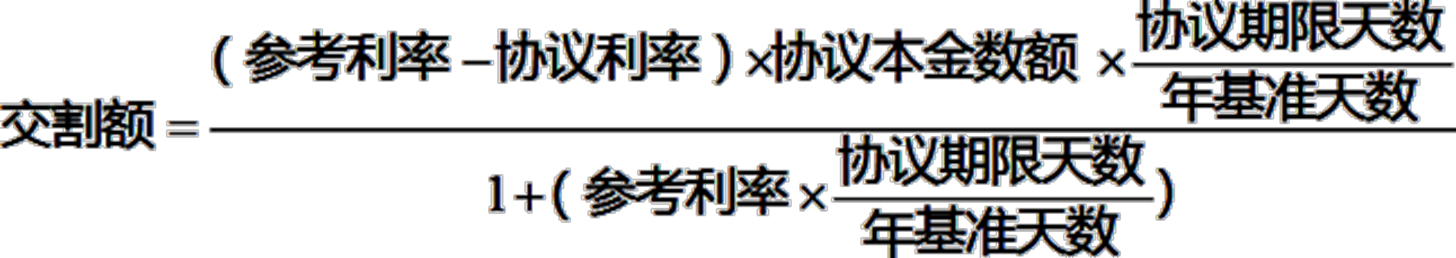
一般美元的年基准天数取360天,英镑的年基准天数取365天。
参考利率一般选取被广泛接受的市场利率,如美国是担保隔夜融资利率(SOFR)。
若参考(市场)利率>协议(约定)利率,交割额为正,卖方向买方支付交割额;
若参考利率<协议利率,交割额为负,买方向卖方支付交割额。
2远期利率协议的估值
远期利率协议与其他远期合约一样,在签订时理论价值为零,因此其协议利率等于远期利率(iF),计算公式为:
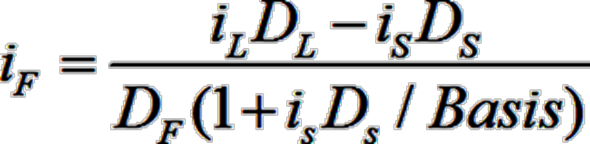
若期初协议利率不等于远期利率, 则可以通过构造套利策略获取无风险利润,在现实生活中,银行通常以远期利率为基准,将报出的买(卖)价格下浮(上浮)一定数量的基点。

远期合约的套期保值
由于远期合约是由银行提供的场外交易产品,合约不规范,流动性较差,因此远期合约用于套期保值主要是静态套期保值。
在期初签订远期合约,后通过到期交割的方式完成套期保值,目的是完全消除套期保值期间价格波动的风险。
多头套期保值是买入远期合约的套期保值,空头套期保值指卖出远期合约的套期保值。
1. 基于远期利率协议的套期保值
某公司计划在3个月之后借入一笔为期6个月的1000万美元的浮动利率债务。根据该公司的信用状况,该公司能以6个月期的LIBOR利率水平借入资金,目前6个月期的LIBOR利率水平为6%,但该公司担心3个月后LIBOR将上升。
为此,它可以买入一份名义本金为1000万美元的3×9远期利率协议。假设现在银行挂出的3×9以LIBOR为参照利率的远期利率协议的报价为6.25%,那么该借款者就可以把借款利率锁定在6.25%的水平上。

2. 基于远期外汇合约的套期保值
多头套期保值就是通过买入远期外汇合约来避免汇率上升的风险,
它适用于在未来某日期将支出外汇的机构和个人,如进口商品、出国旅游、到期偿还外债、计划进行外汇投资等。
空头套期保值就是通过卖出远期外汇合约来避免汇率下降的风险,
它适用于在未来某日期将收到外汇的机构和个人,如:出口商品、提供劳务、现有的对外投资、到期收回贷款等。
当两种货币之间没有合适的远期合约时,套期保值者可利用第三种货币来进行交叉套期保值。

金融期货的价格
金融期货主要包括股指期货、货币期货和利率期货等。
期货价格定义为使期货合约价值为零的理论交割价格。
由于期货是在场内进行的标准化交易,其逐日盯市制度、每日结清浮动盈亏的制度决定了期货在每日收盘后理论价值归为零, 即期货的报价相当于远期合约的协议价格,故期货的报价理论上等于标的资产的远期价格。
事实上由于交易制度的规定,理论报价在远期价格的基础上需要进行一定的调整。


金融期货的套期保值
1 完全套期保值
类似远期合约,如果投资者希望套期保值的现货资产的种类和规模能够与市场上交易的期货的标的资产种类以及期货规模相匹配,可以进行类似远期合约的完全套期保值。
例如,一家美国公司想为2022年12月15日要支付的2500万欧元进行套期保值,已知12月份交割的欧元期货合约规模为12.5万欧元,则公司可以通过买入200份欧元期货合约进行完全套期保值。
在实际运用中,套期保值的效果会受到以下三个因素的影响:
• ①需要避险的资产与期货标的资产不完全一致;
• ②套期保值者不能确切地知道未来拟出售或购买资产的时间,因此不容易找到时间完全匹配的期货;
• ③需要避险的期限与避险工具的期限不一致。
在这些情况下,必须考虑基差风险、合约的选择和最优套期保值比率等问题。
2 基差风险与套期保值工具的选择
基差(Basis)=待保值资产的现货价格-用于保值的期货价格
如果打算进行套期保值的资产与期货的标的资产一致,在期货到期日时,期货价格将收敛到现货价格,因此基差会趋于0,但在到期日之前,基差可正可负。基差变动带来的风险称之为基差风险。
为了降低基差风险,要选择合适的期货合约,它包括两个方面:
• ①选择合适的标的资产;
• ②选择合约的交割月份。
选择标的资产的标准是标的资产价格与保值资产价格的相关性。
相关性越好,基差风险就越小。
因此选择标的资产时,最好选择保值资产本身,若保值资产没有期货合约,则选择与保值资产价格相关性最好的资产的期货合约。
在选择合约的交割月份时,要考虑是否打算实物交割。对于大多数金融期货而言,实物交割的成本并不高,在这种情况下,通常应尽量选择与套期保值到期日相一致的交割月份,从而使基差风险最小。
若套期保值者不能确切地知道套期保值的到期日,也应选择交割月份靠后的期货合约。
3 最优套期保值比率的确定
套期保值比率是指期货合约的总价值与套期保值资产现货总价值之间的比率,即一单位现货头寸保值者所建立的期货合约单位。
若QF表示一份期货合约的价格,N表示期货的份数, NS表示待保值资产的价值,则:

当套期保值资产价格与标的资产的期货价格相关系数等于1时,为了使套期保值后的风险最小,套期保值比率应等于1。
而当相关系数不等于1时,套期保值比率就可能不等于1。
(1)最优套期保值比率的理解。
无论多头套期保值还是空头套期保值,都有:
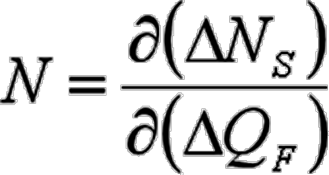
• 这个公式体现了期货最优套期保值比率的本质含义:期货到期时,期货价格每变动1单位时,被套期保值的现货价格变动的量就是最优套期保值比率应确定的期货份数。反过来也就意味着1单位的现货需要N单位的期货头寸对其进行套期保值,才能达到最优的消除风险的效果。
(2)货币期货的最优套期保值比率
货币期货的套期保值方向选择与外汇远期是相同的,当面临外币汇率上升带来的损失时,可以买入该外币的期货;相反则卖出该外币的期货。
到目前为止,学术界和实务界已经提出了多种估计最优套期保值比率的方法,最常见也比较具有一般性的是“最小方差套期保值比率”,即套期保值的目标是使得整个套期保值组合收益的波动最小化的套期保值比率,具体体现为套期保值收益的方差最小化。
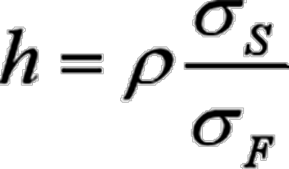
货币期货在方差最小的情况下,其最优套期保值比率为:

用上述比率配置外汇期货进行套期保值,可以使组合价值变动最小,即在方差意义下风险最小,此时期货的最佳数量为:
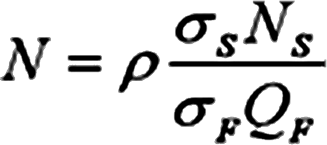
(3)股指期货最佳套期保值数量
当用股指期货为股票组合套期保值时,股指期货最佳套期保值数量(N)为:
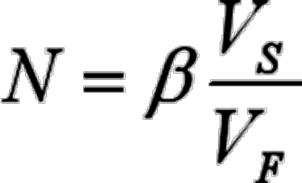
其中,Vs 为股票组合的价值;VF为单位股指期货合约的价值(等于期货价格乘以合约大小);β为该股票组合的β值。因为股票组合没有单位价格,因此很少使用套期保值比率,直接计算套期保值需要的期货数量即可。
某公司打算运用6个月期的S&P500股价指数期货为其价值500万美元的股票组合套期保值,该组合的β值为1.8,当时的期货价格为400。由于一份该期货合约的价值为400×500=20万美元,因此该公司应卖出的期货合约的数量为:

(4)利率期货与久期套期保值
利用利率期货进行套期保值方向与远期利率协议是完全相反的,因为利率期货以债券或者短期存款为标的,当利率上升时,债券价格或者短期存款的价格是下跌的。因此投资者担心利率上升带来的损失时,要卖出利率期货,这样当利率上升时,利率期货价格下跌,利率期货空头可以获益,用以弥补利率上升带来的损失。相反,当投资者担心利率下降带来的损失时,要买入利率期货。
由于当市场利率变动时,债券价格的变动幅度取决于该债券的久期,而利率期货价格的变动幅度也取决于利率期货标的债券的久期,因此我们可以根据保值债券与标的债券的久期来计算套期保值比率。
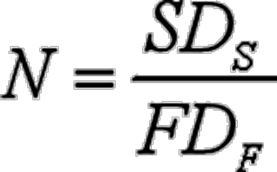
令S和DS分别表示需进行套期保值资产的价格和久期,F表示利率期货的价格,DF表示期货合约标的债券的久期。则为了对冲收益率变动对保值债券价值的影响,所需要的期货合约数(N)为:

2023年11月20日,某基金管理者持有2000万美元的美国政府债券,他担心市场利率在未来6个月内将剧烈波动,因此他希望卖空2024年6月到期的长期国债期货合约,假设国债的面值为 100 美元,一份国债期货合约对应于1000 份国债,即一份国债期货对应于10万美元的国债。该合约目前市价为94.1875美元,那么每份合约价值94187.50美元。假设需保值的债券平均久期为8年,长期国债期货合约的平均久期为10.3年。则为进行套期保值,他应卖空的期货合约数为:
注意:基于久期的套期保值是不完美的,存在着较多的局限性,它没有考虑债券价格与收益率关系曲线的凸度问题,而且它是建立在收益率曲线平移的假定上,因此在实际运用时要多加注意。
4 滚动套期保值
由于期货合约的有效期通常不超过1年,而套期保值的期限有时又长于1年,在这种情况下,就必须采取滚动的套期保值策略,即建立一个期货头寸,待这个期货合约到期前将其平仓,再建立另一个到期日较晚的期货头寸直至套期保值期限届满。如果交易者通过几次平仓才实现最终的套期保值目的,则交易者将面临几个基差风险。

金融期货的套利
金融期货可以利用基差的变动规律进行:
期现套利(现货与期货反向操作进行套利的方式,利率期货和股指期货市场应用较多)
跨期套利(在同一期货品种不同期限的期货间进行)
跨市场套利(在外汇期货市场进行)。
1 期现套利
它是利用期货价格与标的资产现货价格的差异进行套利的交易,即在现货市场买入(卖出)现货的同时,按同一标的资产,以同样的规模在期货市场上卖出(买入)该资产的某种期货合约,并在未来一段时间后同时平仓的交易。
由于期货价格理论近似于远期价格,而远期价格又决定于标的资产的现货价格,因此期货价格与现货价格存在着强相关性,当期货价格与现货价格偏离超过理论差距时就会产生套利机会,可以通过期货和现货方向相反、头寸相同的方式进行套利。
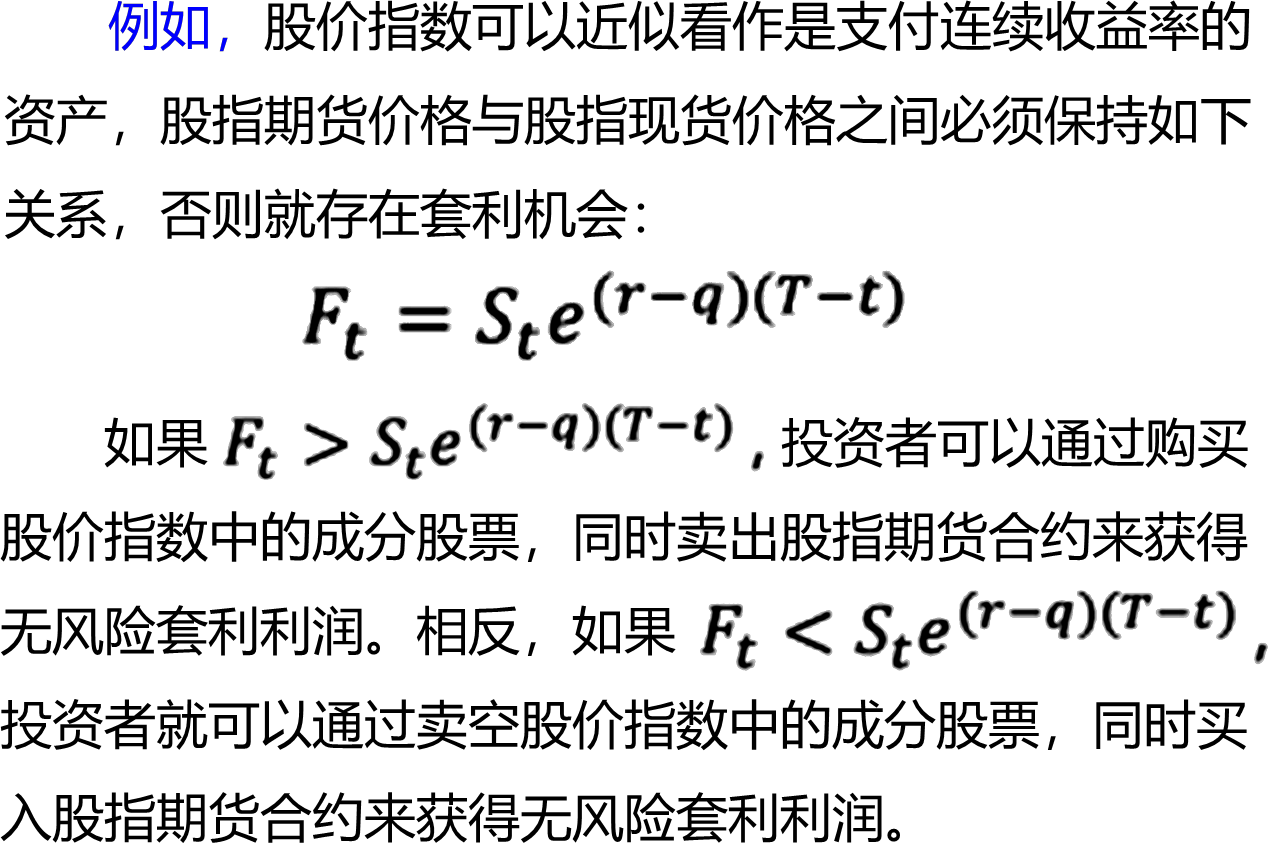
2 跨期套利
跨期套利是指在同一期货市场(如股指期货)的不同到期期限的期货合约之间进行的套利交易,
具体来说,就是买入(卖出)某一较短期限的期货合约的同时, 卖出(买入)另一相同标的资产的较长期限的期货合约,在较短期限的期货合约到期时或到期前同时将两个期货合约对冲平仓的交易。
跨期套利在同一市场进行,且期货市场没有卖空限制,因此跨期套利是套利交易中使用较多的策略。
跨期套利依赖的指标就是基差,当基于同一标的资产的不同期限的期货合约报价产生的基差差异超出正常范围时,可以通过跨期套利获取无风险利润。
3 跨市场套利
跨市场套利是指利用同一种期货合约在不同交易所之间的价差而进行的套利交易。
具体来说,就是在买入(卖出)某一交易所的某一期货合约的同时,按同一数量、同一到期期限卖出(买入)另一交易所的同一期货合约,并在未来某一时间同时将两种期货合约对冲平仓的交易。
货币期货中使用较多。

利率互换的定价
利率互换是指买卖双方同意在未来的一定期限内根据同种货币的同样的名义本金交换现金流。
其中一方的现金流根据浮动利率计算,而另一方的现金流根据固定利率计算,
通常双方只交换利息差,不交换本金。
互换的期限通常在1年以上,有时甚至在15年以上。
普通利率互换可以由一组远期利率协议复制,也可以由固定利率债券和浮动利率债券的组合复制,因此利率互换的价值等于债券组合的价值,可以运用债券组合对互换进行定价。
以利率互换的买方为例,利率互换的买方支付固定利率,获得浮动利率,因此可以将买方的收益等价于其发行了一个固定利率的债券,购买了一个浮动利率的债券,故其价值为:
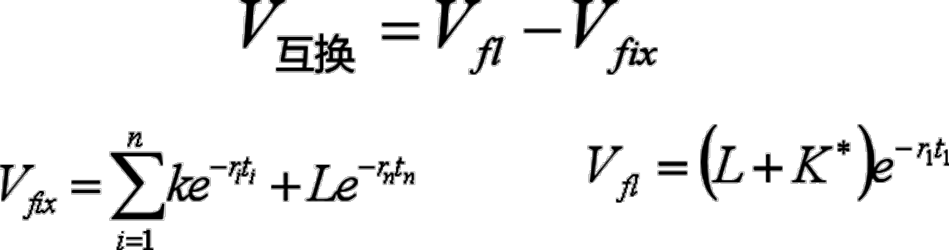

货币互换的定价
货币互换是买卖双方将一种货币的本金和利息与另一种货币的本金和利息进行交换的协议。
货币互换的买方在期初获得外币,并将等值的本币借给卖方;
在合约期限内买方支付外币利息,获取本币利息;
合约到期时买方向卖方偿还外币本金,同时获得本币的本金。
由此可见,货币互换与利率互换在结构和运作机制上相似,但它们是两种不同的互换合约,其主要不同在于以下三个方面。
• (1)利率互换只涉及一种货币,而货币互换要涉及两种货币。
• (2)在协议开始和到期时,货币互换双方常常交换本金,而利率互换不涉及本金的交换。
• (3)货币互换双方的利息支付可以均为固定利率,也可以均为浮动利率,或者固定利率与浮动利率互换,而标准利率互换多见于固定利率与浮动利率互换。
定义V互换为货币互换买方的价值,那么:
V互换=BD-S0BF
BF 是用外币表示的从互换中分解出来的外币债券的价值;
BD是从互换中分解出来的本币债券的价值;
S0是即期汇率(外币兑本币,如人民币为本币,美元为外币,1美元=6.2人民币元,则S0 =6.2)。
对于付出本币利息,收入外币利息的那一方。即卖方,即价值为: -V互换= S0BF-BD

金融互换的套利
金融互换的套利运用的是比较优势原理。
|
英国 |
法国 |
|
|
产能 |
小麦 8份/天 |
小麦 3份/天 |
|
鱼 4份/天 |
鱼 3份/天 |
|
|
单独工作2天(无合作) |
小麦11份,鱼7份 |
|
|
合作2天 |
小麦16份,鱼6份 |
|
互换是比较优势理论在金融领域最生动的运用。根据比较优势理论,只要满足以下两种条件,就可以通过互换进行套利:
① 双方对对方的资产或负债均有需求;
② 双方在两种资产或负债上存在比较优势。
1 利率互换的套利
假设A、B公司都想借入5年期的1000万美元借款,A公司想借入与6个月期相关的浮动利率借款,B公司想借入固定利率借款。但两家公司信用等级不同,故市场向它们提供的利率也不同。
|
表8-4 市场提供给A、B两家公司的借款利率 |
|
固定利率 浮动利率 |
|
A公司 6.00% 6个月期 Libor+0.30% |
|
B公司 7.20% 6个月期 Libor+1.00% |
|
注:表中的利率均为一年计一次复利的年利率。 |
A公司 6.00%, Libor+0.30%
B公司 7.20%, Libor+1.00%
A公司在固定利率市场上存在比较优势,7.20%-6.00%=1.2%
B公司在浮动利率市场上存在比较优势,
(Libor+1.00%)-(Libor+0.30%)=0.7%
套利利润= 1.2%-0.7%= 0.5%
A公司和B公司可以通过如下互换分享无风险利润,降低双方的融资成本:

A 、B 两家公司通过利率互换套利如图8-7所示。

A 公司融资成本Libor + 6% - 6% = Libor ,(浮动);
B 公司融资成本6% + Libor + 1% - Libor = 7% ,(固定)。
互换前:
A公司 6.00%, Libor+0.30%
B公司 7.20%, Libor+1.00%
互换后:
A 公司节约成本Libor + 0.3% - Libor = 0.3% ,
B 公司节约成本7.2% -7% = 0 .2% ,
A 、B 公司通过利率互换分别获利0 .3% 和0. 2%。
2 货币互换的套利
假设英镑和美元汇率为1英镑 =1.5 美元。
A公司想借入5年期的1000 万英镑借款,
B公司想借入5年期的1500 万美元借款。
|
表8-5 市场向A、B两家公司提供的借款利率 |
||
|
美元 |
英镑 |
|
|
A公司 |
8.00% |
11.6% |
|
B公司 |
10.00% |
12% |
|
A- B |
-2% |
-0.40% |
A公司 $8.00%, £11.6%
B公司 $10.00%, £12.00%
A公司在美元市场上存在比较优势,10.00%-8.00%=2.00%
B公司在英镑市场上存在比较优势, 12.00%- 11.6%=0.4%
套利利润= 2.00%-0.4%= 1.6%
A公司在货币互换中支付英镑利息,获得美元利息,同时在市场上借入美元借款;
B公司在货币互换中支付美元利息,获得英镑利息,同时在市场上借入英镑借款。

互换前:
A公司 $8.00%, £11.6%
B公司 $10.00%, £12.00%
互换后:
A公司融资英镑的成本为8%+10.8%-8%=10.8%;
B公司融资美元成本为8%+12%-10.8%=9.2%,
A公司、B公司均节约了0.8%的成本。
总结:
1、对外,买自己有比较优势的;
2、对内,支付对方自己想要的;
3、分利,有说明按说明,无说明,双方平分。



运用货币互换管理汇率风险
货币互换可以用来转换资产或债务组合的货币构成,在全球各市场之间进行套利,从而一方面降低筹资者的融资成本或提高投资者的资产收益,另一方面促进全球金融市场的一体化。

金融期权的价值结构
期权费也可称为期权价格、期权的权利金,指的是期权交易中的价格,即购买期权的一方为自己获得的买入标的资产或卖出标的资产的权利预先支付给期权卖方的费用。
期权费由两部分构成:内在价值和时间价值。
1 内在价值
内在价值指期权按执行价格立即行使时所具有的价值, 一般大于0。
看涨期权,内在价值相当于标的资产现价与执行价格的差;
看跌期权,内在价值相当于执行价格与标的资产现价的差。
2 时间价值
时间价值指的是期权费减去内在价值部分以后的余值。
在实务中,所有期权的出售方都无一例外地要求买方支付的期权费高于期权的内在价值。
原因:期权的非对称性表明期权卖方具有亏损的无限性和盈利的有限性特征,需要对卖方所承担的风险予以补偿。
期限越长的期权,基础资产价格发生变化的可能性越大,因而期权的时间价值越大。
在执行价格既定时,期权费大小与期权的期限长短呈正相关关系。
期权越临近到期日,时间价值就越小,这种现象被称为时间价值衰减。
当期权临近到期日时,在其他条件不变的情况下,其时间价值下降速度加快,并逐渐趋向于0, 一旦到达到期日,期权的时间价值将为0。

金融期权价格的合理范围
1. 欧式看涨期权价格的合理范围
由于看涨期权赋予的是买入标的资产的权利,因此其价格不会超过标的资产自身的价格,否则,套利者可以通过购买标的资产并出售买权,轻易获得无风险利润。
同时由于期权时间价值是非负的,因此其价格也不会低于内在价值,故欧式看涨期权的期权费收值的合理范围为:
ma× [St - Xe –r(T-t), 0 ]≤C ≤ St
St 为标的资产的现价;X 为期权的执行价格;
e 为自然对数的底;r为无风险利率;t为当前时间;T为期权到期时间;c为欧式看涨期权的期权费。
由于欧式期权不能提前执行,因此,其内在价值通过折现进行了调整。
2. 欧式看跌期权价格的合理范围
由于看跌期权赋予的是以固定价格X卖出标的资产的权利, X 是执行看跌期权带来的最高收益,故看跌期权的价格应低于执行价格,而欧式看跌期权无法提前执行,因此其价格要低于最高收益的折现值; 否则, 套利者可以通过出售卖权并将所得收入以无风险利率进行投资,获得无风险收益。
同时,看跌期权的时间价值也是非负的,故其期权费也不会低于其内在价值。
综合上述分析,欧式看跌期权的期权费取值的合理范围为:
ma× [Xe –r(T-t)-St , 0 ]≤p ≤ Xe –r(T-t)
P为欧式看跌期权的期权费。
3. 美式看涨期权价格的合理范围
在标的资产没有红利支付时, 美式看涨期权虽然可以提前执行,但提前执行获得的资产不产生红利,而货币可以产生时间价值,因此提前执行美式看涨期权是不合理的,其价值的合理范围与欧式看涨期权相同。
不过当标的资产有红利或者利息支付时, 美式看涨期权是可能提前执行的。
4. 美式看跌期权价格的合理范围
由于提前执行看跌期权相当于提前卖出资产,获得现金,而现金可以产生无风险收益,因此直观上看, 美式看跌期权可能提前执行,故美式看跌期权的价格通常大于欧式看跌期权,而其取值范围也相应扩大为:
ma× (X -St ,0 )≤p ≤ X
否则,套利者可以以低于期权内在价值的价格购入期权,然后马上行使期权来获得无风险利润。
p 为美式看跌期权的期权费。

金融期权的套期保值
1. 利用期权为现货资产套期保值
当未来需要买入现货资产,但却担心未来价格上涨增加购买成本时,可以买入看涨期权进行套期保值;
当未来需要卖出现货资产,但却担心未来价格下跌降低资产收益时,可以买入看跌期权进行套期保值。
2. 期权的动态套期保值
由于金融期权合约到期损益的不对称性,期权价格与其影响因素之间产生了非线性关系,因此如果投资者的资产组合中包含了售出的期权,为了控制无限的亏损可能,需要对期权产品进行动态套期保值,当影响因素如标的资产价格发生变化时需要及时调整标的资产的头寸,以达到更好的套期保值的目的。
影响期权价格的因素主要包括:标的资产价格、标的资产的波动率、无风险利率、到期期限、执行价格五个因素,除执行价格外其他因素都是变动的,故期权套期保值需要考虑各个因素的变动。
期权的套期保值也被称为希腊字母套期保值。

金融期权的套利
1. 看涨期权与看跌期权之间的套利
看涨和看跌期权合理的价格范围可知,当看涨期权和看跌期权价格在上述价格范围之外时,就会存在套利机会,可以通过买卖标的资产和期权设计套利策略赚取无风险利润。
相同标的资产、相同到期日以及相同执行价格的欧式看涨期权和l欧式看跌期权之间还应该满足平价关系:
c + Xe –r(T-t)= St +p
如果不能满足上述等式,就可以设计套利策略获取无风险利润。
假设某投资者认为某一股票的价格在以后的3个月中将发生重大变化,该股票的现行市场价值为69美元,该投资者可以通过同时购买到期期限为3个月,执行价格为70美元的一个看涨期权和一个看跌期权来进行套利。假定看涨期权的成本为4美元,看跌期权的成本为3美元。如果到期时股票价格保持69美元不变,则该策略的成本为6美元(初始投资7美元,此时看涨期权到期价值为0,看跌期权到期价值为1美元)。如果到期时股票价格为70美元,则会有7美元的损失(这是可能发生的最坏情况)。但是,如果股票价格跳跃到90美元,则该策略可获利13美元;如果股票价格跌到55美元,可获利8美元。

2. 垂直价差套利
相同标的资产、相同期限、不同协议价格的看涨期权的价格或看跌期权的价格之间存在一定的不等关系, 一旦在市场交易中存在合理的不等关系被打破,则存在套利机会,这种套利被称为垂直价差套利,包括蝶式价差套利、盒式价差套利、鹰式价差套利等。
以蝶式价差套利为例。
考虑三种协议价格X1 、X2 和X3,相同标的资产, 相同到期日的看涨期权,X2 =(X1 + X3)÷ 2 ,利用套利定价原理可以推导出三者的期权应该满足: 2C2 < C1 +C3, 当该关系不满足时,可以通过买入执行价格为X1和X3的期权,卖出执行价格为X2的期权进行套利。
假定某一股票的现价为61美元,如果某个投资者认为这以后的6个月中股票价格不可能发生重大变化。假定6个月期看涨期权的市场价格见表:
|
执行价格(美元) |
看涨期权的价格(美元) |
|
55 |
10 |
|
60 |
7 |
|
65 |
5 |
通过购买一个执行价格为55美元的看涨期权,购买一个执行价格为65美元的看涨期权,同时出售两个执行价格为60美元的看涨期权,投资者就可以构造一个蝶式价差期权。
构造这个期权组合的成本为10+5 -(2×7)=1美元。
|
执行价格(美元) |
看涨期权的价格(美元) |
操作 |
|
55 |
10 |
购买1份(-10) |
|
60 |
7 |
卖出2份(2×7) |
|
65 |
5 |
购买1份(-5) |
如果在6个月后,股票价格高于65美元或低于55美元,该策略的收益为0,投资者的净损失为1美元。
如果股票价格在56〜64美元之间,运用该策略就可以获利。当6个月后股票价格为60美元时,会得到最大利润4美元。
|
执行价格及方向 |
到期日价格<55 |
56 |
60 |
64 |
到期日价格>65 |
|
买入看涨(55)1份 |
0 |
1 |
5 |
9 |
15 |
|
卖出看涨(60)2份 |
0 |
0 |
0 |
-8 |
-20 |
|
买入看涨(65)1份 |
0 |
0 |
0 |
0 |
5 |
3. 水平价差套利
水平价差套利是利用相同标的资产、相同协议价格、不同期限的看涨期权或看跌期权价格之间的差异来赚取无风险利润。
一般说来,虽然欧式期权只能在有效期结束时执行,但期限较长的期权价格仍应高于期限较短的期权;否则就存在无风险套利机会。
典型的如日历价差交易策略,即买入期限较长的期权,同时卖出期限较短具有相同标的资产、相同行使价格的期权进行套利。
4. 波动率交易套利
标的资产的波动率是期权定价中最难以确定的因素,如果知道期权的价格,通过期权定价公式反向求解,可以计算出标的资产的一个波动率,称为期权的隐含波动率。
隐含波动率过高则意味着期权相对昂贵,如果过低,期权就会相对便宜。
由于波动率具有可预测性,因此可以通过预测波动率与隐含波动率的比较确定期权价值的涨跌,
如预测波动率高于隐含波动率,则未来期权价值应该增加,反之应该降低。
由于看涨期权和看跌期权价值均与波动率正相关,且相同执行价格的看涨、看跌期权的隐含波动率应该相等。 因此一般可以通过看涨和看跌期权的组合进行套利,即跨式组合套利。
预测>隐含,买入看涨期权和看跌期权,即跨式组合多头套利;否则,可以通过卖出看涨期权和看跌期权进行套利,即跨式组合空头套利。


