方差和标准差的概念、计算和应用包括哪些

很多情况下，我们不仅需要了解数据的期望值和平均水平，还要了解这组数据分布的离散程度。分布越散，其波动性和不可预测性也就越强。尤其对于投资者而言，不仅关心投资的期望收益率，也关心实际收益率相对预期的收益率可能有多大的偏差，即该投资回报的风险水平。对于投资收益率r，用方差(σ²)或者标准差(σ)来衡量它偏离期望值的程度。其中，σ²=E(r-Er)²，它的数值越大，表示收

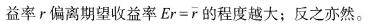
假设从历史数据或者模型模拟得出收益率，．的离散分布，其方差和标准差计算公式为：

其期望收益率，这意味着该产品的7日年化收益率非常稳定，投资者可以在该产品上获得持续稳定的回报，而不容易遭受损失，但也难以获取超常收益。
方差和标准差除了应用于分析投资收益率，还可以用来研究价格指数、股指等的波动情况。例如，我们选取上证指数(Index)2014年4月每日收盘价后，可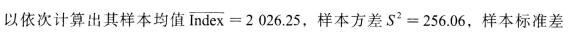 

S=16．01。这些数值可以协助后续的分析工作，如估计指数日波动幅度在特定范围内的概率大小等。