金融资产的收益与衡量
金融资产的收益与衡量相关课程
 金融资产的收益与衡量考点解析
金融资产的收益与衡量考点解析
 金融资产的收益与衡量介绍
金融资产的收益与衡量介绍
金融资产的收益:
利息、股息与红利等现金流收益和资产买卖价差收益。
买卖价差收益也称资本利得。
简化收益率公式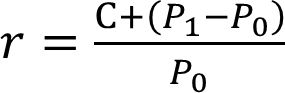
r为收益率,C为金融资产的现金流收益,P0为资产的期
初价格,P1 为资产的期末价格。
为了让收益率能够在相同期限下具有可比性,常见的三种处理方法:
①算术平均法计算的收益率
表8-1 某基金案例 单位:亿元
|
项目 |
第1年 |
第2年 |
第3年 |
第4年 |
|
期初资产总额 |
1 |
1.2 |
2.0 |
0.8 |
|
持有期收益率 |
10% |
25% |
-20% |
20% |
|
净现金流入前的总资产 |
1.1 |
1.5 |
1.6 |
0.96 |
|
净现金流入 |
0.1 |
0.5 |
-0.8 |
0.6 |
|
期末管理资产总额 |
1.2 |
2.0 |
0.8 |
1.56 |
算术平均法计算的收益率为(10%+25%-20%+20%)÷4=8.75%
②几何平均法计算的收益率

几何平均法计算的时间加权平均收益率rG为7.19%
③资金加权平均收益率
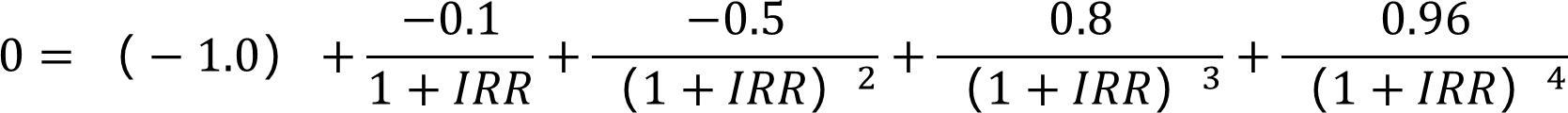
把投资的现金流看做公司财务中的资本预算来计算得出的内部收益率。
对于不同到期期限的金融资产,或投资者的持有周期不一样的,为让各自收益率能够避免期限的影响而具有可比性,使用年化利率。年化利率有两种计算方式,单利和复利。
单利方法计算的年化利率=每个时间段利率×每年包含的时间段个数
1+ 复利方法计算的年化利率=(1+每个时间段利率)每年包含的时间段个数
相关知识点pdf资料
金融资产的收益与衡量考点试题
正确答案: D
答案解析: 金融资产收益的不同也直接决定了金融资产价格的差异,为使不同金融资产的收益情况具有可比性,收益率成为最常见的衡量指标,该指标是金融资产收益与购买金融资产现值之比。
正确答案: B
答案解析: 为了让收益率能够在相同期限下具有可比性,常见的处理方法主要有三种,使用 三种方法,分别得到算术平均法计算的收益率、几何平均法计算的收益率以及资金加权平均收益率。
正确答案: D
答案解析: 持有时间较短(不超过1 年)的债券,直接按债券持有期间的收益额除以买入价计算持有期收益率:r=(Pn-P0+C)/P0
其中,r为持有期收益率,C为债券票面收益(年利息),Pn为债券的卖出价格,P0为债券的买入价格。
所以r=(101-100+5)/100=0.06=6%
正确答案: B
答案解析: 该债券的现金流收益(年利息)=1000×10%=100(元)
该债券的期末价格-期初价格=1000-900=100(元)
收益率=(100+100)/900=22.22%。
大咖讲解:金融资产的收益与衡量

收益率
(一)金融资产的收益与衡量
金融资产的收益:
利息、股息与红利等现金流收益和资产买卖价差收益。
买卖价差收益也称资本利得。
简化收益率公式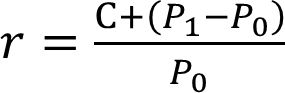
r为收益率,C为金融资产的现金流收益,P0为资产的期
初价格,P1 为资产的期末价格。
为了让收益率能够在相同期限下具有可比性,常见的三种处理方法:
①算术平均法计算的收益率
表8-1 某基金案例 单位:亿元
|
项目 |
第1年 |
第2年 |
第3年 |
第4年 |
|
期初资产总额 |
1 |
1.2 |
2.0 |
0.8 |
|
持有期收益率 |
10% |
25% |
-20% |
20% |
|
净现金流入前的总资产 |
1.1 |
1.5 |
1.6 |
0.96 |
|
净现金流入 |
0.1 |
0.5 |
-0.8 |
0.6 |
|
期末管理资产总额 |
1.2 |
2.0 |
0.8 |
1.56 |
算术平均法计算的收益率为(10%+25%-20%+20%)÷4=8.75%
②几何平均法计算的收益率

几何平均法计算的时间加权平均收益率rG为7.19%
③资金加权平均收益率
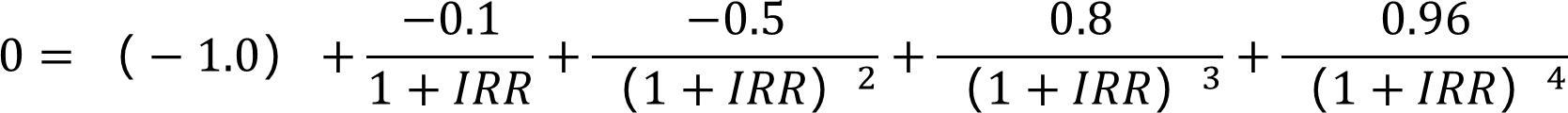
把投资的现金流看做公司财务中的资本预算来计算得出的内部收益率。
对于不同到期期限的金融资产,或投资者的持有周期不一样的,为让各自收益率能够避免期限的影响而具有可比性,使用年化利率。年化利率有两种计算方式,单利和复利。
单利方法计算的年化利率=每个时间段利率×每年包含的时间段个数
1+ 复利方法计算的年化利率=(1+每个时间段利率)每年包含的时间段个数
名义收益率是指包含物价变动因素的利率;
实际收益率是指剔除通货膨胀或通货紧缩的利率。
例题:设 2022 年猪肉价格为 20 元/斤, 2023 年涨至21 元/斤,对应的通货膨胀率为 5% 。名义收益率10%。
2022 年,按照 20 元/斤的价格1万元可购买 500 斤猪肉,
2023 年,按照 21元/斤的价格1.1万元可购买 523.81 斤猪肉,
从实际购买力的角度来看,这笔投资的实际收益率为(523.81-500) ÷500 = 4.76%
精确的实际收益率
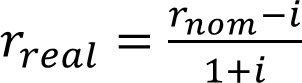
近似的实际收益率
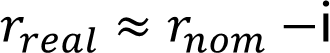
通货膨胀率为i,名义收益率为rnom,实际收益率为rreal

资本资产定价模型的假设与含义
资本资产定价模型(CAPM )是在资本市场处于均衡状态的价格决定模型。
CAPM 基于两组假设,分别与投资者行为和市场结构相关。
投资者行为方面的假设:
① 投资者都是厌恶风险的,同时具有不满足性, 即任何投资者都希望财富越多越好;
② 投资者都追求期末财富的期望效用最大化;
③ 所有投资者对未来都具有一致性预期,都能正确地认识到所有资产的收益服从联合正态分布;
④ 投资者都是理性的,都追求"均值——方差"最优化;
⑤ 所有投资者均可免费获得信息,市场的信息是公开的、完备的。
市场结构方面的假设:
① 所有资产均为责任有限的,即对任何资产,其期末价值总是大于或等于0;
② 市场是完备的,即不存在交易成本和税收,且所有资产均可以无限分割;
③ 存在无风险资产,投资者可以以共同的无风险利率进行借贷,且不受数量限制;
④ 存在做空机制,投资者可以做空所有资产;
⑤ 市场处于完全竞争状态,即不存在垄断和操纵,资本市场有众多的投资者,每一个个体投资者的买入或卖出行为,都不会影响资产的价格。
在CAPM 的假设下,最优风险组合就等于市场组合。
市场组合包含了市场上流通的所有证券,其中,每一个证券的投资比例等于它们的相对市场价值,即该证券的市场价值除以所有证券的市场价值总和。
理论上,市场组合包含所有风险资产:
金融资产如股票、债券、 期权、期货等,以及实际资产如不动产、黄金、古董、艺术品等。
市场组合就是资本配置线与风险资产有效边界的切点。
资本市场线给出了每一种证券组合的风险水平的应得收益,即任何一种证券组合的预期收益率 E(rp) 和标准差 σ(rp) 关系应该符合资本市场线的关系。
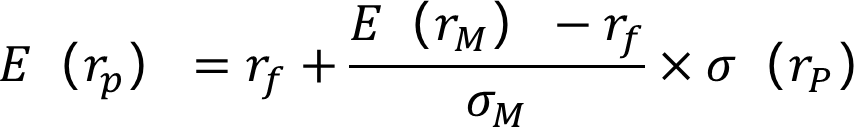
E(rM) 表示市场组合的预期收益率、σM市场组合的标准,rf无风险利率。
整理后得到
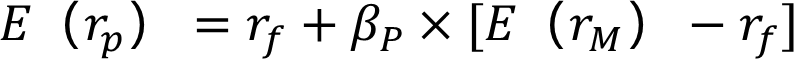
βp 通常被称为证券组合P的贝塔系数。
表明资产的风险溢价E(rp)-rf 等于该资产贝塔系数乘以市场组合的风险溢价。

通货膨胀率与实际收益率
名义收益率是指包含物价变动因素的利率;
实际收益率是指剔除通货膨胀或通货紧缩的利率。
例题:设 2022 年猪肉价格为 20 元/斤, 2023 年涨至21 元/斤,对应的通货膨胀率为 5% 。名义收益率10%。
2022 年,按照 20 元/斤的价格1万元可购买 500 斤猪肉,
2023 年,按照 21元/斤的价格1.1万元可购买 523.81 斤猪肉,
从实际购买力的角度来看,这笔投资的实际收益率为(523.81-500) ÷500 = 4.76%
精确的实际收益率
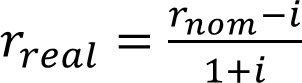
近似的实际收益率
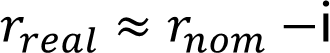
通货膨胀率为i,名义收益率为rnom,实际收益率为rreal

风险与风险溢价
• (一)风险的衡量
风险是指收益的不确定性。
统计学中的方差 Vαr( R) 和标准差 SD(R)为衡量随机变量的不确定性的指标。
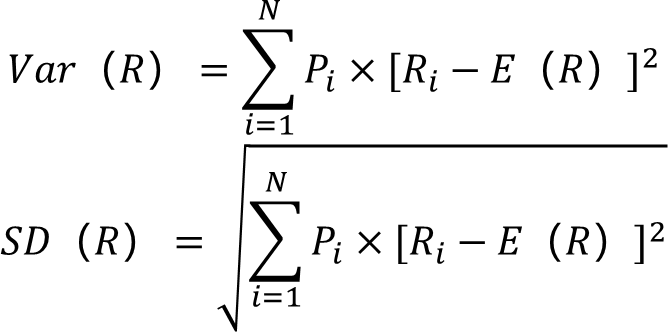
Pi是收益率为Ri时的概率, E(R) 为金融资产的期望收益率(也称预期收益率 ), N为样本事件的个数。
对于已结束的投资,
假设某金融资产在第t期的收益率为rt,T为观测的总期数。
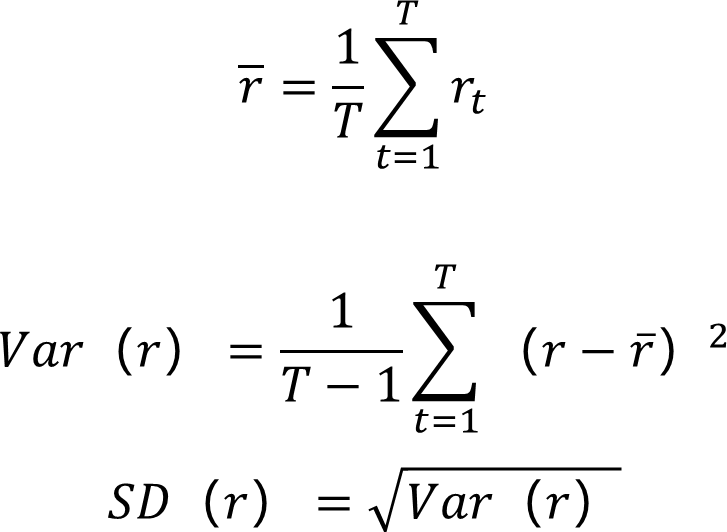
方差和标准差并未考虑量级的因素, 变异系数 CV 也是常用的风险衡量指标。
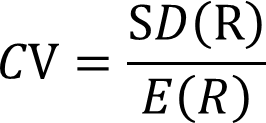
下行风险的衡量
• 投资者可设定一个收益率阈值MARR, 如果实际收益率超过这一收益率阈值,就不视为风险。

σ下行风险为下行风险的刻画指标,Ri为每一期的收益率,N为观测的总期数。
• 最大回撤是另一个常见的刻画下行风险的指标,是指在某一投资组合的特定时间段内,从高点到低点的最大跌幅。
• (二)风险溢价
风险资产的预期收益率与无风险利率之间的差值被称为风险溢价。
无风险利率:国库券的收益率、Shibor等。
超额收益率是指风险资产每一期超过无风险利率的收益率。
• 投资者在进行风险资产选择时,一个基准就是风险溢价是否符合投资者愿意承担的风险程度。
• 利用风险溢价与风险的比值来刻画这一关系
• 常见的指标为夏普比率
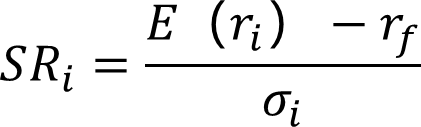
SRi为资产i的夏普比率, E(ri) 为资产i的预期收益率,rf为无风险利率,σi为资产i收益率的标准差。

风险的衡量
风险是指收益的不确定性。
统计学中的方差 Vαr( R) 和标准差 SD(R)为衡量随机变量的不确定性的指标。
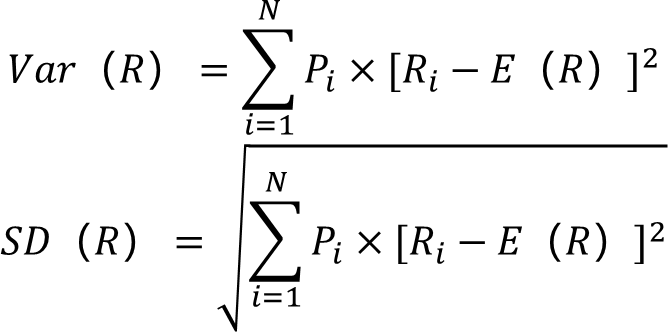
Pi是收益率为Ri时的概率, E(R) 为金融资产的期望收益率(也称预期收益率 ), N为样本事件的个数。
对于已结束的投资,
假设某金融资产在第t期的收益率为rt,T为观测的总期数。
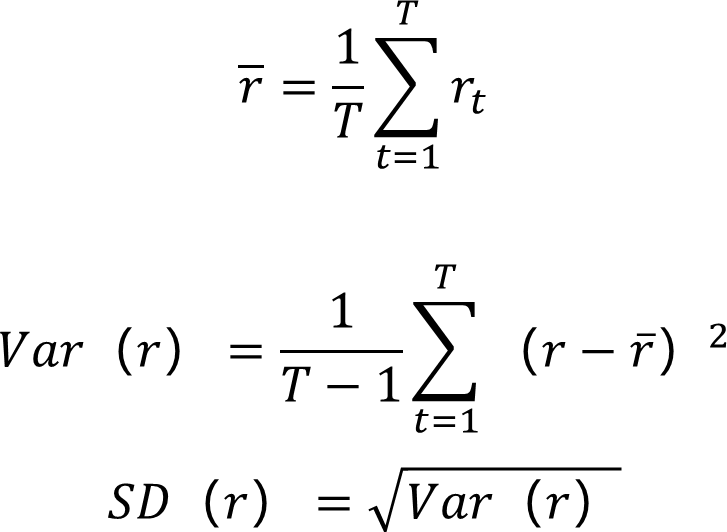
方差和标准差并未考虑量级的因素, 变异系数 CV 也是常用的风险衡量指标。
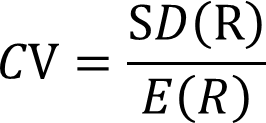
下行风险的衡量
• 投资者可设定一个收益率阈值MARR, 如果实际收益率超过这一收益率阈值,就不视为风险。

σ下行风险为下行风险的刻画指标,Ri为每一期的收益率,N为观测的总期数。
• 最大回撤是另一个常见的刻画下行风险的指标,是指在某一投资组合的特定时间段内,从高点到低点的最大跌幅。

风险溢价
风险资产的预期收益率与无风险利率之间的差值被称为风险溢价。
无风险利率:国库券的收益率、Shibor等。
超额收益率是指风险资产每一期超过无风险利率的收益率。
• 投资者在进行风险资产选择时,一个基准就是风险溢价是否符合投资者愿意承担的风险程度。
• 利用风险溢价与风险的比值来刻画这一关系
• 常见的指标为夏普比率
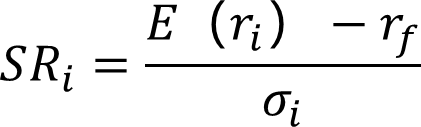
SRi为资产i的夏普比率, E(ri) 为资产i的预期收益率,rf为无风险利率,σi为资产i收益率的标准差。

投资组合与分散风险
资产配置:投资者根据投资需求,将投资资金在不同资产类别之间进行分配,即为资产配置。
资产配置的最基本形式:
是将投资组合分为风险资产与无风险资产。
投资组合中投资于风险资产的部分,取决于投资者的风险厌恶程度。
(一)两种风险资产之间的资产配置
投资者在债券与股票之间进行投资组合,将ϖ比例的资金投入债券基金,将(1- ϖ) 比例的资金投入股票基金。债券基金和股票基金的收益率分别为 rB rS ,债券基金和股票基金的收益率的标准差分别为 σB 和σS,两者收益率的相关系数为ρ ,该投资组合的收益率 rp 和标准差 SD (rp) 分别为:
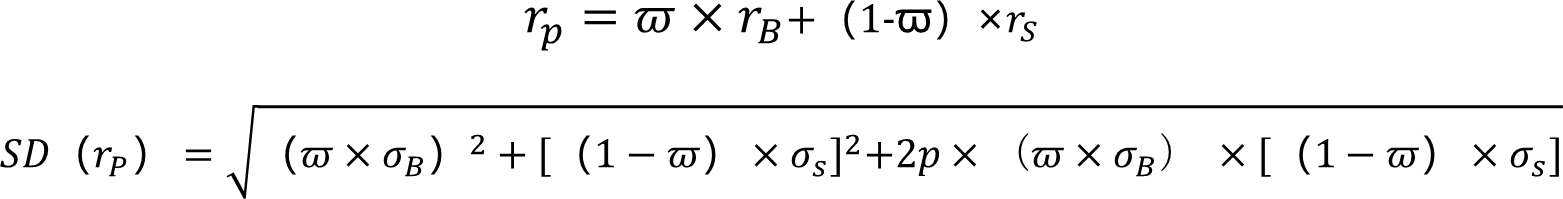
在相关系数较低甚至为负的情形下,可以降低投资组合的风险。
【例】假设债券基金预期收益率 E( rB) =5%, 股票基金预期收
益率 E( rs) =10%,σB=8%, σs=20%,ρ=0.2
投资比例为债券基金和股票基金各占50%。
投资组合预期收益率 E( rp) 和标准差计算如下:
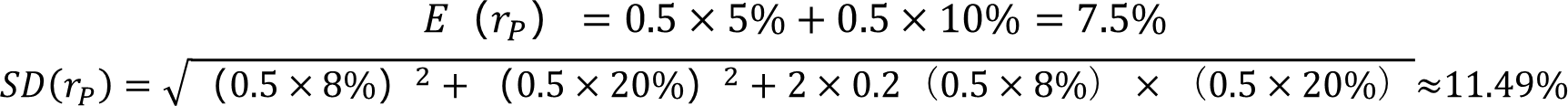
结论:分散投资,降低了风险。
投资组合还可以通过调整两种风险资产的比例,使投资者拥有更多不同的"收益一风险"组合,在允许做空的环境下,组合的范围将进一步扩大。
所有可行的投资组合的“收益一风险”集合被称为可行集。
两种风险资产配置下的可行集是一条弓形曲线。
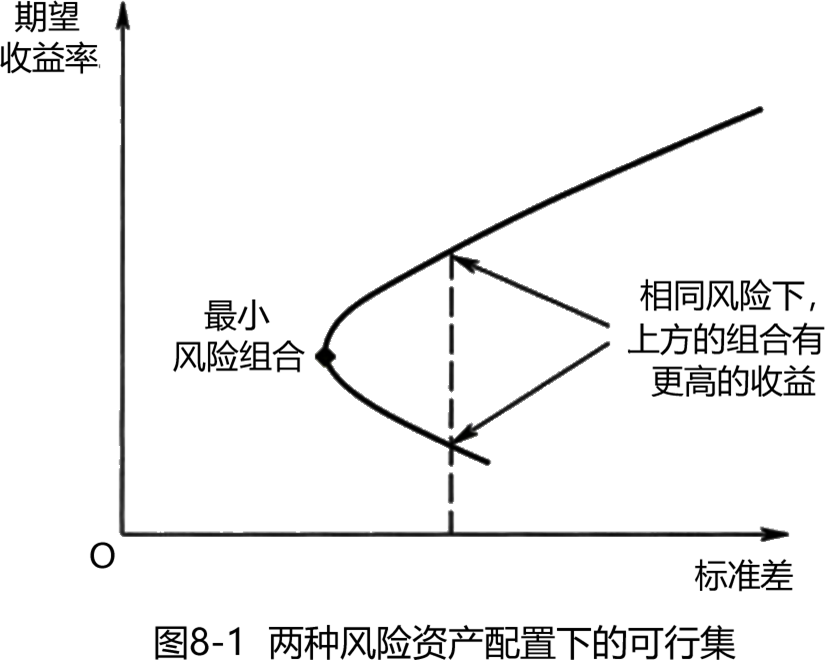
• (二)多种风险资产的资产配置
风险相同,选高收益;收益相同,选低风险。
对应于可行集区域左上方的曲线,即N点到 B点的曲线,这条曲线也被称为有效边界,处于有效边界上的组合称为有效组合。
N点对应方差最小的组合,其代表的组合被称为最小方差组合。

• 有效边界的特点:
①有效边界是一条向右上方倾斜的曲线,反映了“高风险、高收益"的原则;
②有效边界是一条向上凸的曲线;
③有效边界曲线上不可能有凹陷的地方。
• (三)无风险资产与风险资产的资产配置
无风险资产的标准差为0,无风险资产和风险资产间的相关系数也为0。风险资产的收益率和标准差分别为 rp 和σp,投资于风险资产的比例为ϖ,投资组合预期收益率E(rc) 和标准差 σ(rc )为
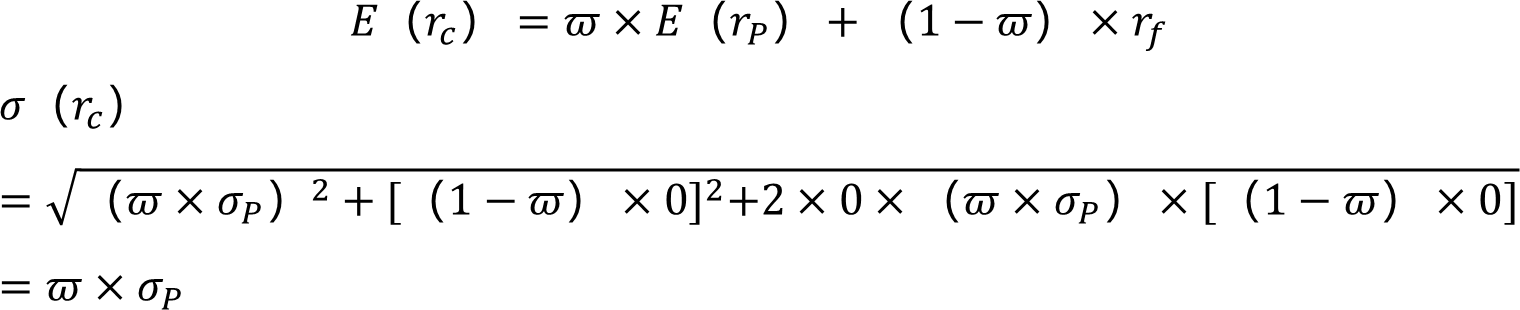
将两式整理,得到
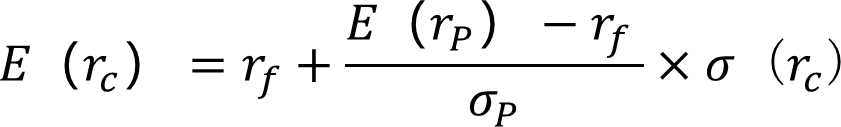
投资组合的预期收益率与风险呈直线关系,该直线被称为资本配置线(CAL)。
资本配置线特征:
①该直线经过(0,rf) 点;
②该直线的斜率为风险资产的夏普比率。
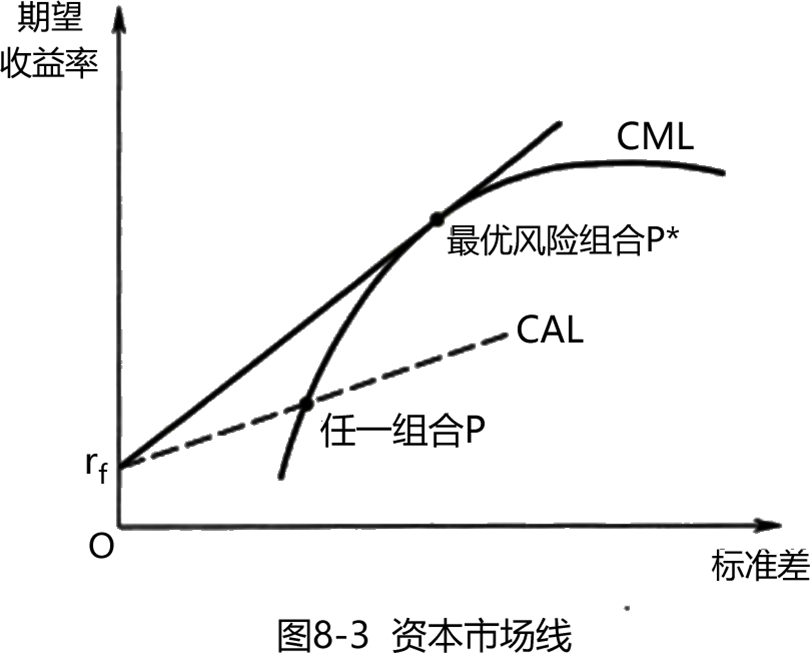
由于有效边界上的每个点都是一种风险资产组合,因此,无风险资产可以与有效边界上的任一点进行投资组合,并相应地形成一条资本配置线。
CAL 斜率越大,其对应的风险资产组合就会使投资者的效用越高,该风险资产组合也被称为最优风险组合。
由(0,rf)这一点射出的、与有效边界相切的直线被称为资本市场线( capital market line , CML)。
切点对应的风险资产组合就是最优风险组合。 由于资本市场线最偏向左上方,因此其斜率最大,即对应于最优风险组合的夏普比率最大。
通常资本市场线向上倾斜,说明随着风险的增加,预期收益率将成比例地增加。
风险资产组成的最优风险组合的确定与投资者的风险偏好无关,就是最优风险组合。

两种风险资产之间的资产配置
投资者在债券与股票之间进行投资组合,将ϖ比例的资金投入债券基金,将(1- ϖ) 比例的资金投入股票基金。债券基金和股票基金的收益率分别为 rB rS ,债券基金和股票基金的收益率的标准差分别为 σB 和σS,两者收益率的相关系数为ρ ,该投资组合的收益率 rp 和标准差 SD (rp) 分别为:
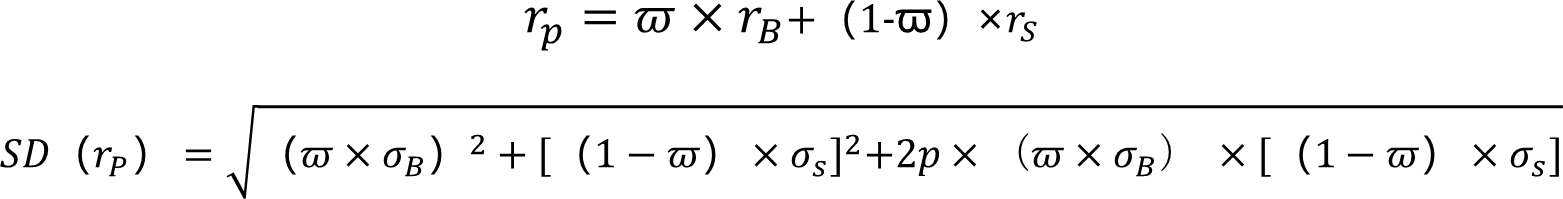
在相关系数较低甚至为负的情形下,可以降低投资组合的风险。
【例】假设债券基金预期收益率 E( rB) =5%, 股票基金预期收
益率 E( rs) =10%,σB=8%, σs=20%,ρ=0.2
投资比例为债券基金和股票基金各占50%。
投资组合预期收益率 E( rp) 和标准差计算如下:
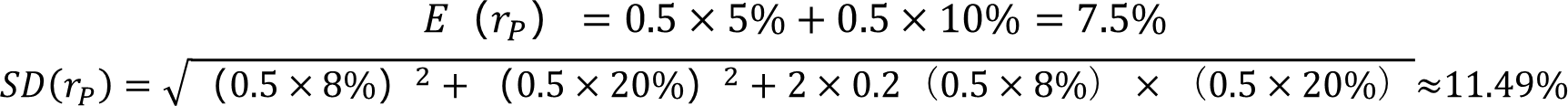
结论:分散投资,降低了风险。
投资组合还可以通过调整两种风险资产的比例,使投资者拥有更多不同的"收益一风险"组合,在允许做空的环境下,组合的范围将进一步扩大。
所有可行的投资组合的“收益一风险”集合被称为可行集。
两种风险资产配置下的可行集是一条弓形曲线。


多种风险资产的资产配置
风险相同,选高收益;收益相同,选低风险。
对应于可行集区域左上方的曲线,即N点到 B点的曲线,这条曲线也被称为有效边界,处于有效边界上的组合称为有效组合。
N点对应方差最小的组合,其代表的组合被称为最小方差组合。

• 有效边界的特点:
①有效边界是一条向右上方倾斜的曲线,反映了“高风险、高收益"的原则;
②有效边界是一条向上凸的曲线;
③有效边界曲线上不可能有凹陷的地方。

无风险资产与风险资产的资产配置
无风险资产的标准差为0,无风险资产和风险资产间的相关系数也为0。风险资产的收益率和标准差分别为 rp 和σp,投资于风险资产的比例为ϖ,投资组合预期收益率E(rc) 和标准差 σ(rc )为
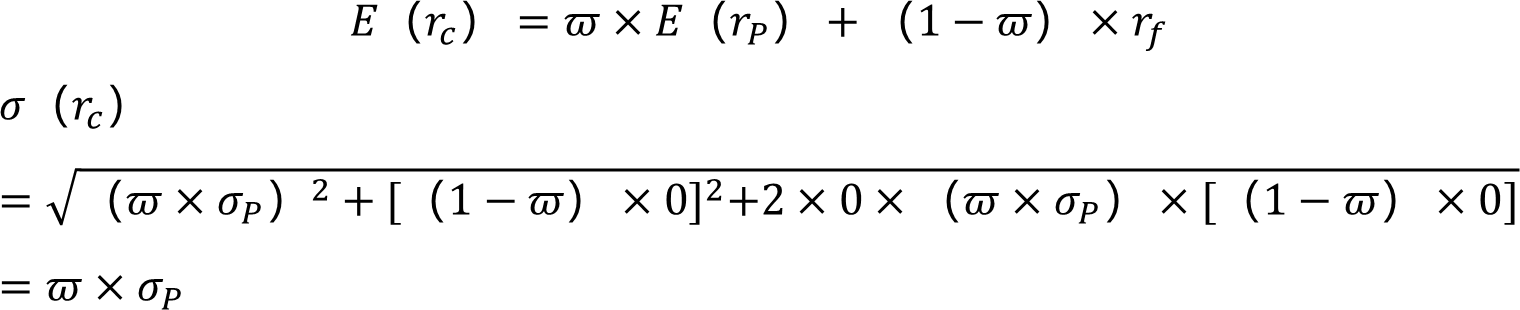
将两式整理,得到
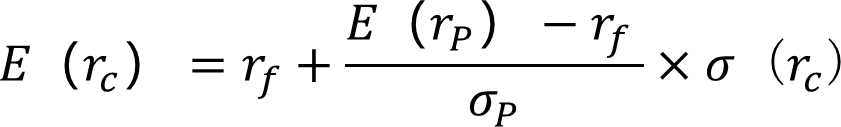
投资组合的预期收益率与风险呈直线关系,该直线被称为资本配置线(CAL)。
资本配置线特征:
①该直线经过(0,rf) 点;
②该直线的斜率为风险资产的夏普比率。

由于有效边界上的每个点都是一种风险资产组合,因此,无风险资产可以与有效边界上的任一点进行投资组合,并相应地形成一条资本配置线。
CAL 斜率越大,其对应的风险资产组合就会使投资者的效用越高,该风险资产组合也被称为最优风险组合。
由(0,rf)这一点射出的、与有效边界相切的直线被称为资本市场线( capital market line , CML)。
切点对应的风险资产组合就是最优风险组合。 由于资本市场线最偏向左上方,因此其斜率最大,即对应于最优风险组合的夏普比率最大。
通常资本市场线向上倾斜,说明随着风险的增加,预期收益率将成比例地增加。
风险资产组成的最优风险组合的确定与投资者的风险偏好无关,就是最优风险组合。
拒绝盲目备考,加学习群领资料共同进步!
师资团队
-

免费听
槐俊升
应试性强,讲的细,效果好
主讲:中级经济基础知识
经济师大神级培训讲师,学员口中YYDS的经济师老师,母题班研究者,培训经验十余年

免费听
葛广宇
记忆魔术师
主讲:初级会计实务,中级财务管理,财务成本管理,中级经济基础知识,初级经济基础知识
副教授,管理学(会计学方向)博士在读、注册会计师,会计师职称。擅长以案例、关键词导向式的教学方法,归纳总结关联考点考点,讲解细致,适合零基础考生,学员称其为“记忆魔术师”。
-

免费听
郑伟
经济学男神
主讲:高级经济实务工商管理,中级经济基础知识,中级工商管理
德国科隆大学经济学博士,就职于北京外国语大学国际教育学院,双语经济学教师。本人学识渊博,底蕴深厚。课堂富有激情,能带动学员学习思维,幽默风趣的大叔型魅力男神。

免费听
王鑫鑫
资深人力资源管理专家
主讲:中级人力资源管理
山东大学MBA,多年从事人力资源管理师一级培训,丰富专业实践教学经验。
-

免费听
陈肖
主讲:中级人力资源管理
中国人民大学硕士、中级经济师、曾就职于500强企业从事管理相关工作。

免费听
李轻舟
主讲:中级建筑与房地产经济
中国建设教育协会专家库专家,高级工程师,全国一级建造师,全国监理工程师,注册执业资格考试老师。
专业智能,高效提分
章节练习
章节专项突破
进入做题
精选试题
省时高效精选
进入做题
模拟考场
海量题免费做
进入做题
考前点题
高效锁分72小时
进入做题
每日一练
每天进步一点点
进入做题
历年真题
真题实战演练
进入做题
易错题
精选高频易错题
进入做题
模考大赛
同场闯关做题
进入做题

APP刷题神器
模考大赛
考点打卡
做题闯关

扫描二维码 下载233网校APP刷题
互动交流

微信扫码关注公众号
获取更多考试资料























