二元回归模型案例
二元回归模型案例相关课程
 二元回归模型案例考点解析
二元回归模型案例考点解析
 二元回归模型案例介绍
二元回归模型案例介绍
多元回归模型在实际应用中,随着自变量个数的增加,即使在有些自变量与因变量完全不相关的情况下,决定系数R2也会增大。为避免因增加自变量个数而高估拟合效果的情况,多元回归模型一般使用修正了自由度的调整后R2(Adjusted R Square)。调整后R2考虑了自变量个数增加带来的影响,在数值上小于R2 。
相关知识点pdf资料

2024年中级经济师《经济基础》经典母题汇总:第十二章
266.51KB
下载
2024年中级经济师《经济基础》经典母题汇总:第十一章
260.02KB
下载
2024年中级经济师《经济基础》经典母题汇总:第十章
277.29KB
下载
2024年中级经济师《经济基础》经典母题汇总:第九章
294.13KB
下载
2024年中级经济师《经济基础》经典母题汇总:第八章
238.08KB
下载
2024年中级经济师《经济基础》经典母题汇总:第七章
273.65KB
下载
2024年中级经济师《经济基础》经典母题汇总:第六章
233.89KB
下载
2024年中级经济师《经济基础》经典母题汇总:第五章
346.95KB
下载
2024年中级经济师《经济基础》经典母题汇总:第三章
324.80KB
下载
2024年中级经济师《经济基础》经典母题汇总:第四章
382.40KB
下载
2024年中级经济师《经济基础》经典母题汇总:第一章
309.08KB
下载
2024年中级经济师《经济基础》经典母题汇总:第二章
567.76KB
下载二元回归模型案例考点试题
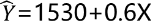 ,R2为0.99,下列说法正确的有( )。
,R2为0.99,下列说法正确的有( )。
正确答案: A
答察解析: 估计的回归方程的回归系数是0.6,显示城镇居民家庭人均可支配收入X每增加1元,城镇居民人均消费Y的平均增加量为0.6元。选项A正确,选项BC错误。将X=20000元代入回归方程,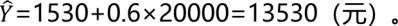 选项E正确。本题中决定系数为0.99,接近于1,可看出回归模型的拟合效果很好,城镇人均可支配收入可以很好地解释人均消费支岀的变化。选项D正确。
选项E正确。本题中决定系数为0.99,接近于1,可看出回归模型的拟合效果很好,城镇人均可支配收入可以很好地解释人均消费支岀的变化。选项D正确。
正确答案: B
答察解析: 二元线性回归 模型:Y=β0+ β 1X1+ β2X2+ε
正确答案: C
答察解析: 二元线性回归模型的调整后R2( Adjusted R Square )=0.63 ,表示受教育年限和职位的二元回归模型对年薪的变化可解释程度为63%。自变量受教育年限和职位的t检验P值0.00529和0.00265都小于0.05,表明2个自变量都通过了t检验,对年薪有显著的线性影响。在相同的职位上,受教育年限(edu)每增长1年,年薪平均增长3669元;相同受教育年限的条件下,管理者(position=1)的年薪比一般职员 ( position=0 )平均增长27 144.47元。已知员工甲受教育年限为10年,在该公司为一般职员,可利用该模型预测其年薪大约为Y =18716+3 669 x 10=55406(元),故B选项错误。
在0.05的显著水平下,不能得出是否有显著的线性影响,只能解释其对年薪是否有显著影响。故A错误。
大咖讲解:二元回归模型案例

回归模型的拟合效果分析
1、模型的检验
一般情况下,在使用估计的回归方程之前,需要对模型进行检验:
①结合经济理论和经验分析回归系数的经济含义是否合理;
②分析估计的模型对数据的拟合效果如何;
③对模型进行假设检验。
2、决定系数R2:也称为拟合优度或判定系数,可以测度回归模型对样本数据的拟合程度。
决定系数是回归模型所能解释的因变量变化占因变量总变化的比例,取值范围为[0,1]
(1)决定系数越高,模型的拟合效果就越好,即模型解释因变量的能力越强。
如果所有观测点都落在回归直线上,R2=1,说明回归直线可以解释因变量的所有变化。
R2=0,说明回归直线无法解释因变量的变化,因变量的变化与自变量无关。
(2)现实应用中R2大多落在0和1之间,R2越接近于1,回归模型的拟合效果越好;R2越接近于0,回归模型的拟合效果越差。
2、回归系数的显著性检验
在大样本假定的条件下,回归系数的最小二乘估计量![]() 和
和![]() ,渐进服从正态分布,可以用t检验方法验证自变量X对因变量Y是否有显著影响。
,渐进服从正态分布,可以用t检验方法验证自变量X对因变量Y是否有显著影响。
t检验的原理是反证法:在原假设![]() (自变量X对因变量Y没有影响)正确的假设下,基于
(自变量X对因变量Y没有影响)正确的假设下,基于![]() 的抽样分布计算一次抽样情况下得到该样本或更极端样本的概率(P值),如果P<0.05,则可以在0.05的显著性水平下拒绝原假设,认为自变量X对因变量Y有显著性影响,即
的抽样分布计算一次抽样情况下得到该样本或更极端样本的概率(P值),如果P<0.05,则可以在0.05的显著性水平下拒绝原假设,认为自变量X对因变量Y有显著性影响,即![]()

模型预测
回归分析的一个重要应用就是预测,即利用估计的回归模型预估因变量数值。
拒绝盲目备考,加学习群领资料共同进步!
师资团队
-

免费听
槐俊升
应试性强,讲的细,效果好
主讲:中级金融,中级经济基础知识
经济师大神级培训讲师,学员口中YYDS的经济师老师,母题班研究者,培训经验十余年

免费听
葛广宇
记忆魔术师
主讲:初级会计实务,中级财务管理,财务成本管理,中级经济基础知识,初级经济基础知识
副教授,管理学(会计学方向)博士在读、注册会计师,会计师职称。擅长以案例、关键词导向式的教学方法,归纳总结关联考点考点,讲解细致,适合零基础考生,学员称其为“记忆魔术师”。
-

免费听
郑伟
经济学男神
主讲:中级工商管理,高级经济实务工商管理
德国科隆大学经济学博士,就职于北京外国语大学国际教育学院,双语经济学教师。本人学识渊博,底蕴深厚。课堂富有激情,能带动学员学习思维,幽默风趣的大叔型魅力男神。

免费听
王鑫鑫
资深人力资源管理专家
主讲:中级人力资源管理
山东大学MBA,多年从事人力资源管理师一级培训,丰富专业实践教学经验。
-

免费听
徐雨光
授课专业,易理解,举例形象
主讲:初级个人理财,中级金融
美国经济学硕士。任职于某高校金融系,主要教学及研究方向为投资理财,教学经验丰富,专业功底深厚,对热点考点把握准确,讲课生动有趣,深入浅出。

免费听
陈肖
主讲:中级人力资源管理
中国人民大学硕士、中级经济师、曾就职于500强企业从事管理相关工作。
专业智能,高效提分
章节练习
章节专项突破
进入做题
精选试题
省时高效精选
进入做题
模拟考场
海量题免费做
进入做题
考前点题
高效锁分72小时
进入做题
每日一练
每天进步一点点
进入做题
历年真题
真题实战演练
进入做题
易错题
精选高频易错题
进入做题
模考大赛
同场闯关做题
进入做题

APP刷题神器
模考大赛
考点打卡
做题闯关

扫描二维码 下载233网校APP刷题
资料包
互动交流

微信扫码关注公众号
获取更多考试资料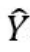 =β0+ β 1X1+ β2X2+(选项不全)
=β0+ β 1X1+ β2X2+(选项不全)





















