三、 随机变量的相关关系 —协方差、相关系数

一、随机变量

（1）随机变量是一个能取得多个可能值的数值变量。

（2）离散型随机变量：如果随机变量X只能取有限个或可数无限多个不同的值，则X为离散型随机变量。

（3）连续型随机变量：如果随机变量X可以取某个区间内的任意实数，则称为连续型随机变量。

二、随机变量的数字特征和描述性统计量

【例题】有下列数字：1，2，3，4，5，6，7，8，9，10

平均数：（1+2+3+4+5+6+7+8+9+10）/10

中位数：大小处于中间的数字，即（5+6）/2

分位数：通常用来研究随机变量X以特定概率取得大于等于（或小于等于）某个值的情况。

如：上25%分位数：10*25%=2.5，即（9+8）/2=8.5

1.随机变量X的期望（均值）

衡量了X取值的平均水平；它是对X所有可能取值按照其发生概率大小加权后得到的平均值。

2.用方差（σ²） 或标准差（σ）来衡量它偏离期望值的程度。

【意义】数值越大，收益率r偏离期望收益率的程度越大，数值越小偏离就越小。

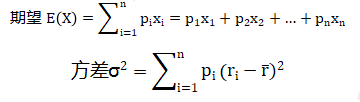
例：某投资者将其资金分别投向A、B、C三只股票，占总资金的比重分别为20%、20%、60%；股票A、B、C的期望收益率分别为R_a=14%、R_b=20%、R_c=8%，则该股票组合的收益率？

  R_p=0.2×14%+0.2×20%+0.6×8%=1.16%

1.正态分布密度函数特点

正态分布图中间高两边低，由中间（X＝μ）向两边递减，并且分布左右对称，是一条光滑的“钟形曲线”。

2.特点：

（1）集中性：数据在均值附近最为集中，距离均值越远，则出现的概率越低。这意味着极端值出现的概率较小，而接近均值的值出现的概率较大。

（2）波动性：正态分布的形状由标准差σ决定，标准差越小，分布越“窄”，数据越集中于均值附近；标准差越大，分布越“宽”，数据的离散程度越大

3.经验法则（称为“68-95-99.7法则”）：约68%的数据落在μ±σ范围内；约95%的数据落在μ±2σ范围内；约99.7%的数据落在μ±3σ范围内。