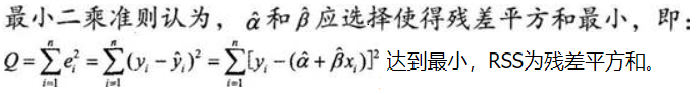一元线性回归分析
一元线性回归分析相关课程
 一元线性回归分析考点解析
一元线性回归分析考点解析
 一元线性回归分析介绍
一元线性回归分析介绍
(一)一元线性回归模型的基本假定
设有如下一元线性回归模型:
![]()
yi:因变量或被解释变量;
χi:自变量或解释变量;
μi:一个随机变量,称为随机(扰动)项;
α,β:是两个常数,称为回归参数,
下标i:表示变量的第 i 个观察值或随机项
t检验
又称回归系数检验,步骤如下:
第一步:提出假设。设原假设 H0:β=0,备择假设H1:β≠0。
第二步:构造t统计量,即服从自由度为n-2的t分布:
![]()


一元线性回归分析的预测:点预测和区间预测
1.点预测。设回归模型为:
yi = α+β xi + μi (i=1, 2 ,3, ..., n)
假定在抽样期外的某预测期 f 中的自变量 xf 已知,上述模型适用于该预测期,这时因变量 yf =α+β xf + μf
其中,随机项满足基本假定。此时 yf 的预测值有两个,一个是期望值,一个是 yf 的点预测值。


期货投资分析知识点:一元线性回归模型的基本假定

期货投资分析知识点:一元线性回归模型的参数估计

期货投资分析知识点:一元线性回归模型的检验-拟合优度

期货投资分析知识点:一元线性回归模型的检验-t检验

期货投资分析知识点:一元线性回归模型的预测
一元线性回归分析考点试题
正确答案: B
答案解析: 拟合优度是反映回归直线与样本观测值拟合程度的量,又称样本“可决系数”,常用R2表示。R2的取值范围为:0≤R2≤1,R2越接近1,拟合效果越好;R2越接近0,拟合效果越差。
正确答案: A
答案解析: 设总生产成本对产量的一元线性回归方程为y=a+bx。由题干可知,x=1000时,yc=30000元;x=0时,yc=6000元。将数据代入方程,解得a=6000;b=24。所以,总生产成本对产量的一元线性回归方程为:yc=6000+24x。
正确答案: D
答案解析: 一元线性回归模型,随机项μ满足以下假定:
假定1:每个μi(i=1,2,3,...n) 均为独立同分布,且服从正态分布的随机变量,E(μi)=0,Var(μi)=σμ2=常数
假定2:每个随机项μi均互不相关,即:
Cov ( μi,μj)=0(i≠ j)
假定3:随机项μi与自变量的任一观察值xi不相关,即:Cov (μi,xi)=0(i=1,2,3,....n)
正确答案: C
答案解析: 拟合优度,又称样本“可决系数”,用于度量回归直线对样本观测值的拟合程度,常用R2表示,计算公式为:
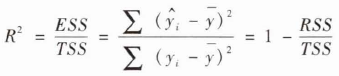
A项为总离差平方和,记为TSS;B项为残差平方和,记为RSS;C项为回归平方和,记为ESS;三者之间的关系为:TSS=RSS+ESS。
大咖讲解:一元线性回归分析


相关性
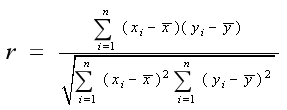

线性回归模型
一元线性回归模型:yi=a+Bxi+μi(i=1,2,3,…,n) 其中,yi称为因变量或被解释变量;xi称为自变量或解释变量;μi是一个随机变量,称为随机(扰动)项;a和β是两个常数,称为回归参数。
多元线性回归主要用于分析影响因变量的因素,不仅涉及一个自变量,而且可能涉及多个自变量。例如,我们在分析一家公众公司的价值时,需要研究其多个财务指标,比如负债比例、资产回报率等指标序列(每个月指标)。这些指标构成公司价值(序列)的核心影响因素,我们定义公司价值(序列)为因变量时,这些财务指标(序列)就是自变量。
多元线性回归主要用于分析影响因变量的因素,不仅涉及一个自变量,而且可能涉及多个自变量。例如,我们在分析一家公众公司的价值时,需要研究其多个财务指标,比如负债比例、资产回报率等指标序列(每个月指标)。这些指标构成公司价值(序列)的核心影响因素,我们定义公司价值(序列)为因变量时,这些财务指标(序列)就是自变量。
多元线性回归分析模型【βk是参数,Xki的线性部分加上随机扰动项μi】
Yi=β0+β1β1i+β2β2i+…+βkXki+μi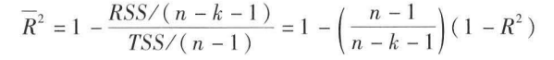

多元线性回归分析
多元线性回归模型分析一个因变量和几个自变量之间的关系。形式如下:


(二)多元线性回归模型的参数估计
同一元线性回归模型类似,可利用OLS估计多元线性回归模型的参数。此时有:
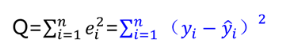
为使得残差平方和Q达到最小的必要条件为:
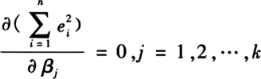
![]()
(三)多元线性回归模型的检验:
1.拟合优度检验
2.F检验(显著性检验)
3.t检验(回归系数检验)
拒绝盲目备考,加学习群领资料共同进步!
师资团队
-

免费听
王佳荣
金融圈达人
主讲:金融市场基础知识,期货基础知识,基金法律法规,中级金融
从事金融类考试培训多年,知名金融培训师、金融机构中层管理、清华大学出版社金融教材副主编、上海人才培训市场促进中心特聘讲师。人称金融类培训界的“一哥”。

免费听
孙婧
外汇分析师
主讲:期货法律法规,投资银行业务(保荐代表人),证券市场基本法律法规,中级法律法规与综合能力,初级法律法规与综合能力
曾就职于多家大型证券、期货公司,具有丰富的金融从业培训经验,外汇分析师,大学生金融交易大赛评委,同时拥有金融类多个从业资格。
-

免费听
李泽瑞
金融培训高级讲师
主讲:证券投资顾问业务,发布证券研究报告业务(证券分析师),初级个人贷款,中级个人贷款,期货投资分析
经济学硕士、金融培训高级讲师,李泽瑞老师从事金融类考证培训,教学经验丰富,出口成“段子”,是一个让学员欲罢不能的很有个人风格的老师,江湖学员称被讲课耽误的“德云社”编外弟子。

免费听
王佳荣
金融圈达人
主讲:金融市场基础知识,期货基础知识,基金法律法规,中级金融
从事金融类考试培训多年,知名金融培训师、金融机构中层管理、清华大学出版社金融教材副主编、上海人才培训市场促进中心特聘讲师。人称金融类培训界的“一哥”。
专业智能,高效提分
章节练习
章节专项突破
进入做题
精选试题
省时高效精选
进入做题
模拟考场
海量题免费做
进入做题
考前点题
高效锁分72小时
进入做题
每日一练
每天进步一点点
进入做题
历年真题
真题实战演练
进入做题
易错题
精选高频易错题
进入做题
模考大赛
同场闯关做题
进入做题

APP刷题神器
模考大赛
考点打卡
做题闯关

扫描二维码 下载233网校APP刷题
互动交流

微信扫码关注公众号
获取更多考试资料