2．等额支付系列情形
（1）终值计算（已知A求F）
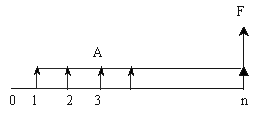
根据该图，可以得到：
F=A+A（1+i）+A（1+i）2+A（1+i）3+……+A（1+i）n－1 （1）
将以上关系式两边同乘以（1+i），得到
F（1+i）=A+A（1+i）+A（1+i）2+A（1+i）3+……+A（1+i）n （2）
将（2）－（1），可得：
Fi= A（1+i）n－A，处理后可得：
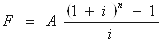
式中
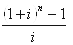称为等额系列终值系数或年金终值系数，用符号（F／A，i，n）表示。于是： F=A（F／A，i，n）
（2）偿债基金计算（已知F求A）
偿债基金计算是等额系列终值计算的逆运算，故可得：
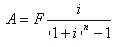
式中
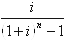称为等额系列偿债基金系数，用符号（A／F，i，n）表示。于是： A＝F（A／F，i，n）
（3）资金回收计算（已知P求A）
由图:
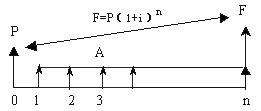
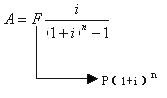
所以:
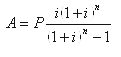
式中
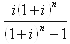称为等额系列资金回收系数，用符号（A／P，i，n）表示。于是： A＝P（A／P，i，n）
（4）现值计算（即已知A求P）
现值计算是资金回收计算的逆运算，故可得：
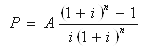
式中
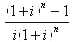称为等额系列现值系数或年金现值系数，用符号(P／A，i，n)表示。于是： P＝A（P／A，i，n）
现在将上述6个公式整合在一起，如下表：
| 公式名称 | 已知项 | 欲求项 | 系数符号 | 公式 |
| 一次支付终值 | P | F | (F/P，i，n) | F=P(1+i )n |
| 一次支付现值 | F | P | (P/F，i，n) | P=F(1+i)－n |
| 等额支付终值 | A | F | (F/A，i，n) |  |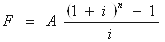
| 偿债基金 | F | A | (A /F，i，n) |  |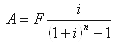
| 资金回收 | P | A | (A/P，i，n) |  |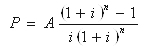
| 年金现值 | A | P | (P /A，i，n) |  |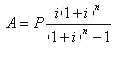
