中级经济师的考生,是不是觉得教材的信息量太大,很多相似内容学过一遍后又凌乱了?老师为大家总结了中级经济师经济基础考点,本文是第二章无差异曲线考点,收藏随时可查看!点击下方图片试听,直接跳转至中级经济师培训班,免费试听专业老师教你如何正确备考>>
一、效用理论
1、经济人假设:假定消费者是追求效用最大化的和理性的,即每一个从事经济活动的人都 是利己的,总是力图以最小的经济代价去获得自己最大的经济利益。经济 人假设是整个经济学的基础。
2、效用:消费者在消费商品或服务时所能感受到的满足程度,是人们的心理感觉, 是主观评价,没有客观标准。
3、基数效用论:该理论认为效用是可以直接度量的,存在绝对的效用量的大小,可以用基数,就是用 1、2、3、4……这些绝对数值来衡量效用的大小。
4、总效用:消费者在一定时期内,从商品或服务的消费中所得到的满足程度总和。总效用 TU=f(Q)一般来说,总效用取决于消费数量的多少,在一定范围内,消费量越大,则总效用就越大。
5、边际效用:消费者增加一个单位商品消费时所带来的满足程度的增 加或者效用的增量。从数学的意义上看,边际效用是总效用的斜率。
6、序数效用论:该理论认为消费者可以知道自己对不同消费组合的偏好次序,用第一、第 二、……这些表示次序的相对数值来衡量效用。
7、基数效用论与序数效用论的关系:①相同点:均用来分析消费者行为,二者得出的分析结论基本是相同的;②不同点:基数效用理论运用边际效用论分析 ,序数效用理论用无差异曲线和预算约束线来分析;基数效用论下效用可加总,即能直接衡量,而序数效用论下效用不能加总,即不能直接衡量。
【提示】边际效用递减的规律:即在一定时间内,随着消费某种商品数量的不断增加,消费者从中得到的总效用是在增加的,但是以递减的速度增加,即边际效用是递减的;当商品消费量达到一定程度后,总效用达到最大时,边际效用为 0;如果继续增加消费,总效用不但不会增加,反而会逐渐减少,此时边际效用变为负数。
二、无差异曲线
1、完备性:如果只有A和B两种组合,消费者总是可以作出,也只能作出下面三种判断中的一种:①对A的偏好大于;②对B的偏好大于A;③对两者偏好无差异。
【提示】完备性保证消费者总可以把自己的偏好准确的表达出来。
2、可传递性:假定有A、B、C三种组合,如果消费者对A的偏好大于 B,对B的偏好又大于C,那么对A的偏好必定大于对C的偏好。
【提示】可传递性可以保证消费者偏好的一致性。
3、消费者总是偏好于多而不是少:如果两组商品的区别只是在于其中一种商品数量的不同,那么消费者总是偏好较多的那个组合,也就是多多益善。
4、无差异曲线的含义:无差异曲线是一条表示能够给消费者带来相同满足程度的两种商品的所有组合的曲线,在这条曲线上的所有各点的两种商品组合带给消费者的满足程度是完全相同的,消费者对这条曲线上各个点的偏好程度是无差异的。
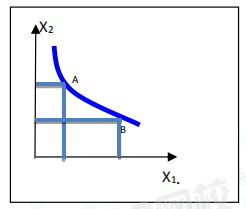
5、无差异曲线的特征
(1)离原点越远的无差异曲线,消费者的偏好程度越高,无差异曲线离原点越远,代表的商品数量越多,根据“多比少好”的假定,消费者得到的满足程度水平越高。

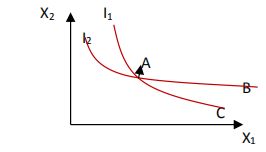
(2)任意两条无差异曲线都不能相交,A、B均位于I2,AB偏好相同;BC均位于 I1,BC偏好相同,根据偏好的可传递性, B与C的偏好相同,但这是不可能的,因为B比C具有更多的X2, B必定比C更受偏好。因此无差异曲线不能相交。
(3)无差异曲线从左向右下倾斜,凸向原点,无差异曲线从左向右下倾斜,斜率为负,这是由商品边际替代率递减规律决定的,商品边际替代率是指在效用水平不变的条件下,消费者增加一单位某商品时必须放弃的另一种商品的数量。无差异曲线上某一点的边际替代率就是无差异曲线上该点的切线斜率的绝对值。
1、关于效用理论的说法,正确的是( )。
A.效用具有客观的标准
B.一般来说,总效用取决于消费数量的大小
C.基数效用论是基于无差异曲线产生的理论
D.边际效用递增是一个普遍趋势


































